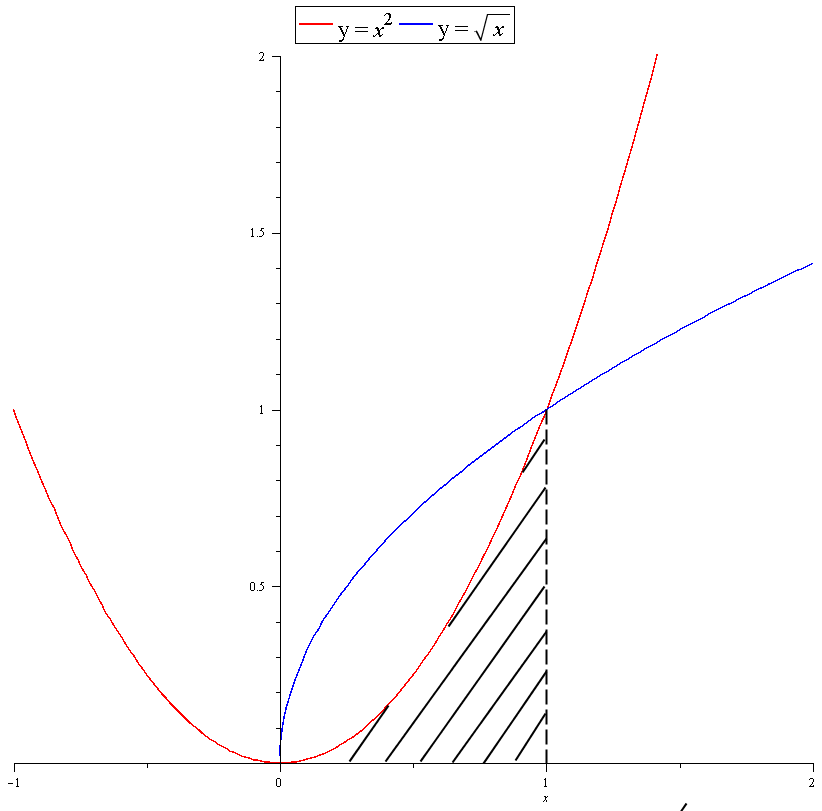
About Beyond simple math and grouping (like "(x2)(x4)"), there are some functions you can use as well Look below to see them all They are mostly standard functions written as you might expectThe base of a solid is the region bounded by the x – axis and the graph of y= V1 – x2 For the solid, each cross section perpendicular to the 2 – axis is a square What is the volume of the solid?In mathematics, a square root of a number x is a number y such that y2 = x;
Solution How To Sketch The Graph Of Y Sqrt X 1
Y=root(1-x^2) graph
Y=root(1-x^2) graph-Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history4/13/21 · Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo


How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange
Range\y=\frac {x^2x1} {x} asymptotes\y=\frac {x} {x^26x8} extreme\points\y=\frac {x^2x1} {x} intercepts\f (x)=\sqrt {x3} f (x)=2x3,\g (x)=x^25,\f\circ \g functionsgraphingcalculator range y=\frac {x^2x1} {x} en1/9/13 · here we have the graph or part of the graph of y is equal to x squared again and I want to find the volume of another solid of revolution but instead of rotating around the xaxis this time I want to rotate around the yaxis and instead of going between 0 and some point I'm going to go between Y is equal to 1 and Y is equal to 4 so I'm going to do is I'm going to take this graph rightI think you're probably reasonably familiar with the idea of a square root but I want to clarify some of the notation that at least what I always found a little bit ambiguous at first I want to make it very clear in your head so when I write if I write a nine under a radical sign I think you know you'll read this as the square root of nine but I want to make one clarification when you just see a number
7/29/10 · If you square both sides of the equation just above, you might recognize the equation as that of a familiar geometric object Keep in mind, though, that you need to graph y = sqrt(a 2 x 2), not the one you get by squaring both sides They are differentSubtracting x^ {2} from itself leaves 0 Subtracting x 2 from itself leaves 0 \left (y\sqrt 3 {x}\right)^ {2}=1x^ {2} ( y 3 x ) 2 = 1 − x 2 Take the square root of both sides of the equation Take the square root of both sides of the equation y\sqrt 3 {x}=\sqrt {1x^ {2}} y\sqrt 3 {x}=\sqrt {1x^ {2}}Evaluate the definite integral abvsolute of fx dx over interval 1,3 by interpreting them in terms of areaThis is an exercise among a collection of selected
Since the given equation y=root(14x^2) restricts y to nonpositive values, the graph is the lower branch of the hyperbola, as shown in Figure 349 The domain of y=root(14x^2) is the set of all x such that 14x^2>=0\begin{align} \mathbf{Area} = \int_{\sqrt{2}}^{\sqrt{2}} (y^2 2) \ dy \\ \mathbf{Area} = \frac{y^3}{3} 2y \bigg _{\sqrt{2}}^{\sqrt{2}} \\ \mathbf{AreaDraw a rough sketch of the graph of the function y = 2 \\sqrt{1 x^2}\ , x ∈ 0, 1 and evaluate the area enclosed between the curve and the xaxis Advertisement Remove


Key To Practice Exam Ii



Implicit Differentiation
6/8/17 · We could also arrive at this conclusion by considering the graph of the function #y^2=4x^2# #x^2y^2=4# Which is a circle centered at #(0,0)# with radius #2# Note that solving for #y# gives #y=pmsqrt(4x^2)#, which is a set of two functions, since a circle by itself does not pass the vertical line test, so a circle is not a function but can be described by a set of #2#Make a rough sketch of the graph of the function y = 4 x^2 , 0 ≤ x ≤ 2 and Sketch the graph of y = root x1 in 0,4 and determine the area of the region Find the area under the curve y = root 6x4 above x axis from x = 0 to x = 2 Draw the rough sketch of y^2 1 = x, x ≤ 2 Find the area enclosed by theBefore trying to jump immediately into plotting, pause to think about the expressions to be plotted Otherwise, you are likely to make silly mistakes and miss the underlying mathematics and beauty One thing that is fairly obvious is that if we sw


How Do You Find The Volume Of Region Bounded By Graphs Of Y X 2 And Y Sqrt X About The X Axis Socratic



Find The Exact Length Of The Curve Y Square Root X X 2 Sin 1 Square Root X Study Com
Use the Shell Method to compute the volume of the solid obtained by rotating the region bound by the graph y=4^2x^2 0 Find the volume of the solid revolved around y5 0 finding the volume of a region using cylindrical shells method 0In other words, a number y whose square (the result of multiplying the number by itself, or y ⋅ y) is x For example, 4 and −4 are square roots of 16, because 42 = (−4)2 = 16 Every nonnegative real number x has a unique nonnegative square root, called the principal square root, which is denoted by x,Roots x^21 Roots Calculator Symbolab This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice Geometry beta


Solution I Wont To Kno How To Graph Y The Square Root Of X 2


Root Tutorials Graphs Multipalette C File Reference
The graph of mathx^2(y\sqrt3{x^2})^2=1/math is very interesting and is show below using desmosSo, to create a table of values for a line, just pick a set of x values, substitute them into the equation and evaluate to get the y valuesA Cartesian coordinate system (UK / k ɑː ˈ t iː zj ə n /, US / k ɑːr ˈ t i ʒ ə n /) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of lengthEach reference line is called a coordinate axis or just axis (plural


Parent Functions And Their Graphs Video Lessons Examples And Solutions
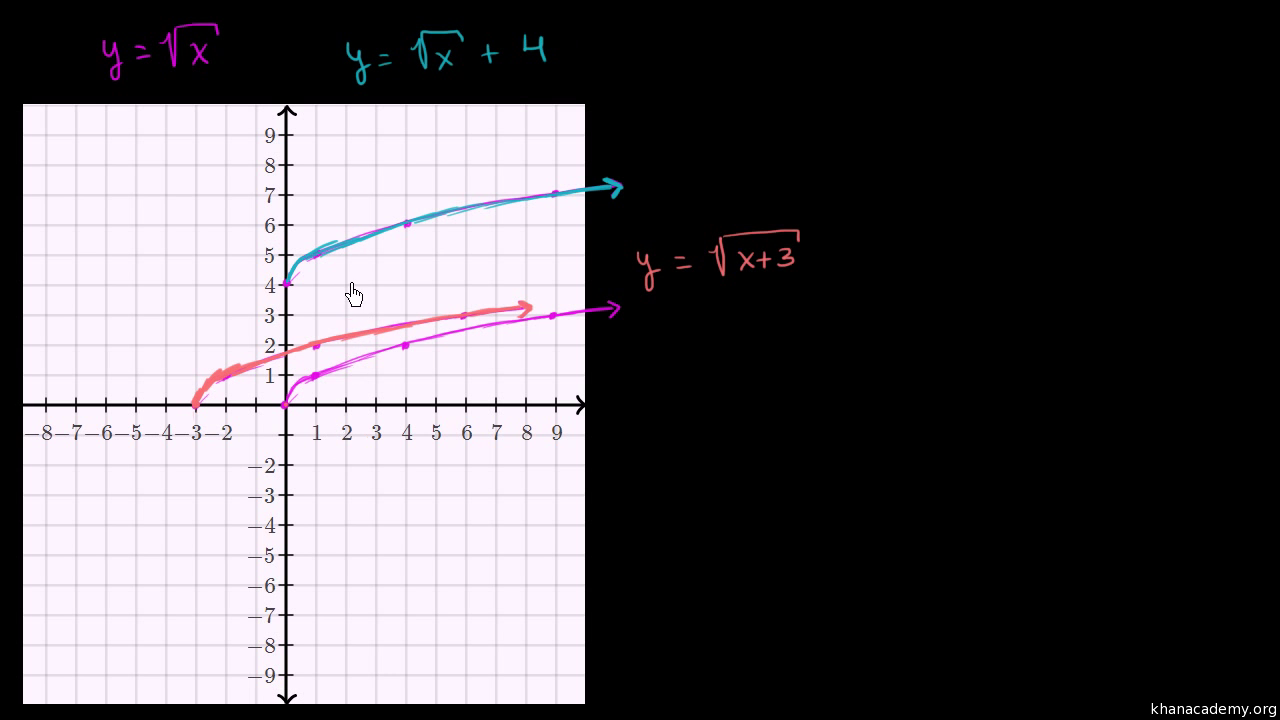


Transforming The Square Root Function Video Khan Academy
3/15/18 · The graph of `y=3x`, with the area under the "curve" between `x=0` to `x=1` shaded When the shaded area is rotated 360° about the `x`axis, aExample Find the area between x = y2 and y = x − 2 First, graph these functions If skip this step you'll have a hard time figuring out what the boundaries of your area is, which makes it very difficult to computeThe calculator will find the tangent line to the explicit, polar, parametric and implicit curve at the given point, with steps shown It can handle horizontal and vertical tangent lines as well


Department Of Mathematics Texas A M University


Derivatives Of Inverse Functions
This equation is in standard form a x 2 b x c = 0 Substitute 1 for a, 1 for b, and 1 − y for c in the quadratic formula, 2 a − b ± b 2 − 4 a c x=\frac {1±\sqrt {1^ {2}4\left (1y\right)}} {2} x = 2 − 1 ± 1 2 − 4 ( 1 − y) Square 1 Square 1 x=\frac {1±\sqrt {14\left (1y\right)}} {2}2,2 \times 2,2\\ 2 z=\sqrt {y x^2 See full answer below3/29/12 · let R be the region bounded by the xaxis, the graph of y=sqrt(x1), and the line x=3 Find the area of the region R calculus The base of a solid is the region in the first quadrant bounded by the graph of y = 3/(e^x) , the xaxis, the yaxis, and the line x=2 Each cross section of this solid perpendicular to the xaxis is a square



Example 4 Graph A Translated Square Root Function Graph Y 2 X 3 2 Then State The Domain And Range Solution Step Graphing Quadratics Function Of Roots


How To Plot The Graph Of Y 1 X 2 Quora
· Ex 92, 4 Verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation 𝑦=√(1𝑥^2 ) 𝑦^′=𝑥𝑦/(1𝑥^2 ) 𝑦=√(1𝑥^2 ) 𝑑𝑦/𝑑𝑥=𝑑(√(1 𝑥^2 ))/𝑑𝑥 =1/(2√(1 𝑥^2 ))×2𝑥 =𝑥/√(1 𝑥^2 ) Now, we have to verify 𝑦^′=𝑥𝑦/(1 𝑥^2 )3/24/17 · y = x² √ (x⁴4x4x³) / 2 (1x) = x² x (x2) / 2 (1x) y = x or x / (1x) or, y = x or 1 1/ (1x) Differentiate wrt x dy/dx = 1 or 1/ (1x)² dome7w and 93 more users foundCharacteristics of Parabolas The graph of a quadratic function is a Ushaped curve called a parabolaOne important feature of the graph is that it has an extreme point, called the vertexIf the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function If the parabola opens down, the vertex represents the highest point on the graph


Horizontal Translation Of Square Root Graphs Expii


What Is The Graph Of X 2 Y 3 X 2 2 1 Quora
3/13/13 · if sqrt(1x2) sqrt(1y2) = a (xy) prove dy/dx=sqrt((1y2)/(1x2)) Maths Continuity and Differentiability(a) Graph (b) Partitioning into how many intervals does insure that can be approximated using Midpoint rule to within ? · Find the point on the graph of function that is closest to the point f(x)=x^2 (2,1/2) Mathematics A sine function has the following key features Period = 4 Amplitude = 3 Midline y=−1 yintercept (0, 1) The function is not a reflection of its parent function over the xaxis Use the sine tool to graph the function



Derivatives Of Inverse Functions
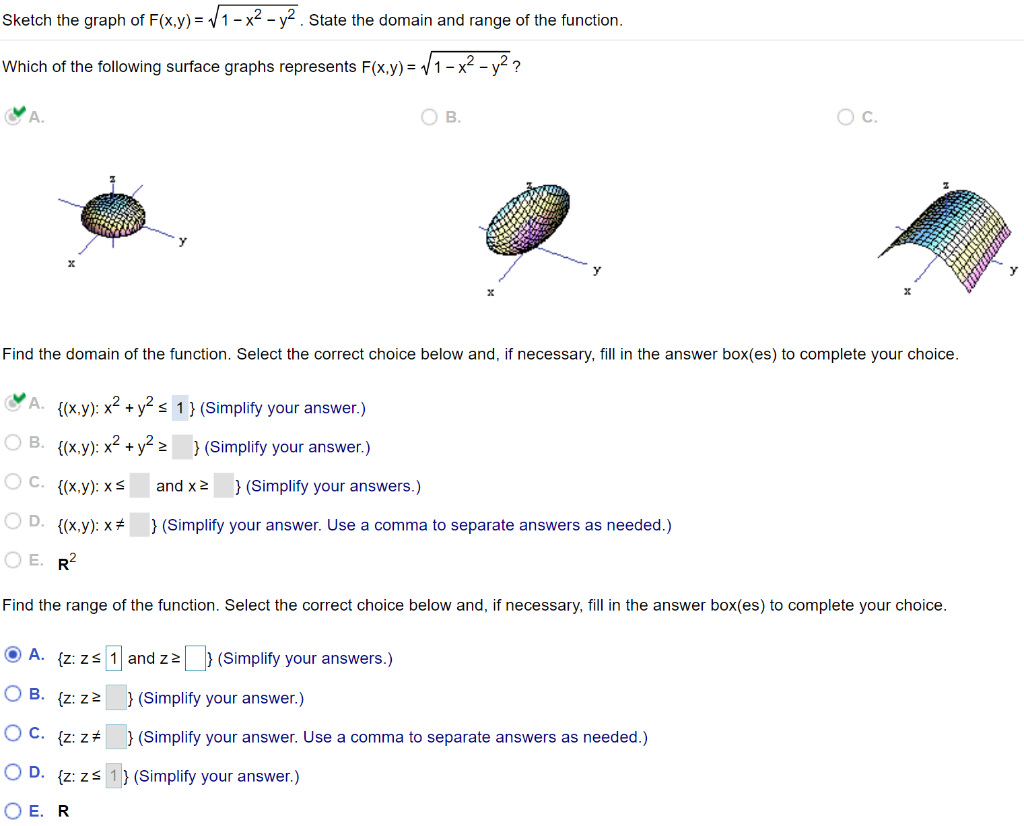


Solved Sketch The Graph Of F X Y Sqrt 1 X 2 Y 2 State Chegg Com
Graph y = 3×2 –x 2 Because the power is a negative quadratic, the power is always negative (or zero) Then this graph should generally be pretty close to the x axisCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history`sqrt(1x^2) sqrt(1 y^2)` = a(x − y) Put x = sin θ, y = sin Φ ∴ θ = sin −1 x, Φ = sin −1 y
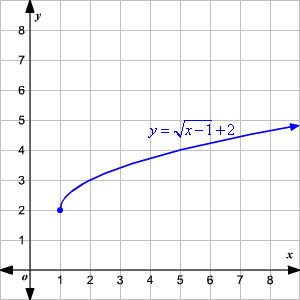


Graphing Square Root Functions



How To Graph Y Sqrt X Video Lesson Transcript Study Com
Select a few x x values from the domain It would be more useful to select the values so that they are next to the x x value of the radical expression end point Tap for more steps Substitute the x x value 2 2 into f ( x) = √ x − 1 f ( x) = x 1 In this case, the point is ( 2, 1) ( 2, 1)Graph the radicand (expression under the radical sign), make a table of values of function f given below, graph f and find its range f( x ) = √ (x 2 4x 6) Solution to Example 7 Use completing the square to rewtite the expression under the square root as follows x 2 4x 6 = (x 2) 2 2 The expression under the square root is always7/24/17 · Observe that, sqrt(1x^2) and sqrt(1y^2) are Meaningful, iff, x le 1, and, y le 1(star^1) This means that, there is no Harm if we let, x=sintheta, and, y=sinphi(star^2) sqrt(1x^2)sqrt(1y^2)=a(xy)," becomes, " costhetacosphi=a(sinthetasinphi) 2cos((thetaphi)/2)cos((theta
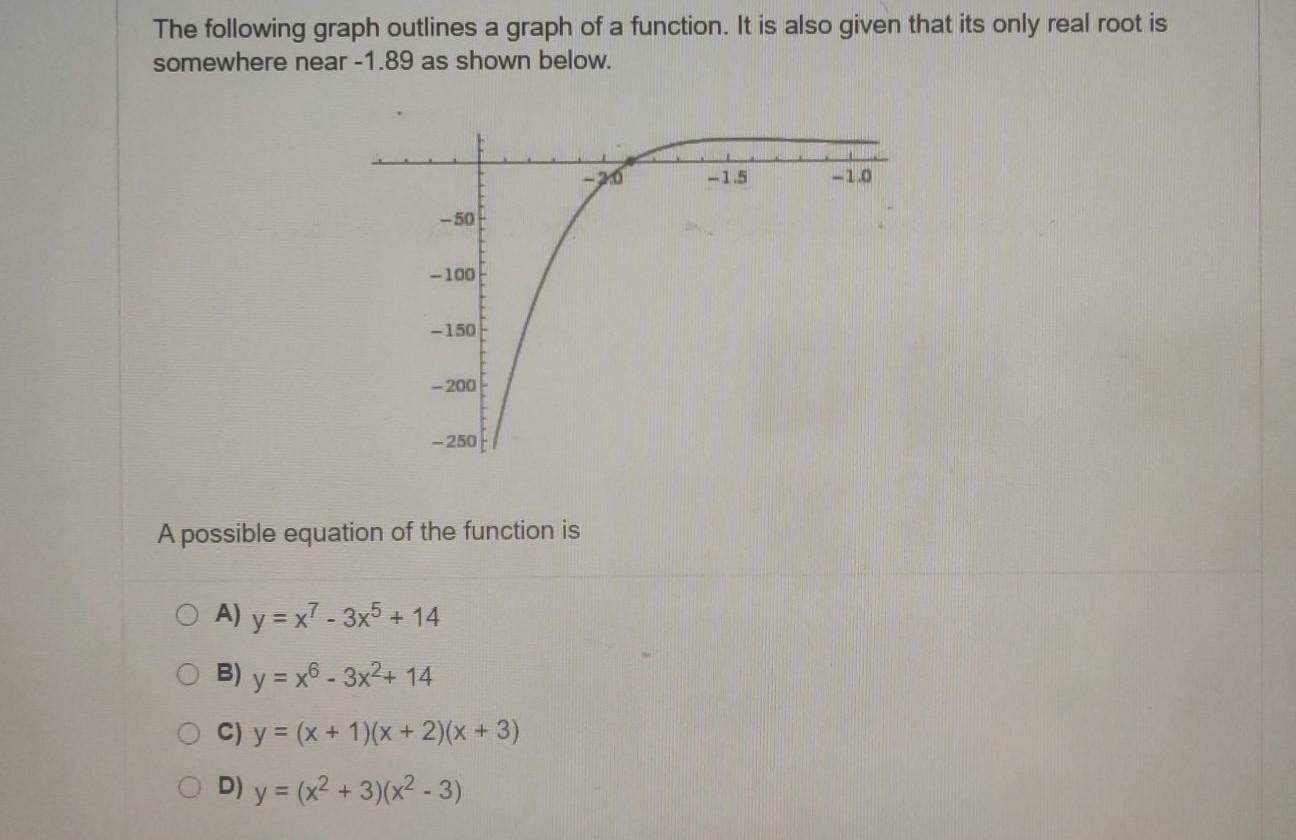


The Following Graph Outlines A Graph Of A Function It Math


Solution Graph F X Square Root Of X Then Use Transformations Of That Graph To Graph H X Square Root Of X 1 2 Label 3 Points On Your Graph
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeIf y= sqrt (1x/1x) provethat (1 – x^2)d y /dx y = 0 if4753 Mark Scheme June 05 Section B 8 (i) At P, x sin 3x = 0 ⇒ sin 3x = 0 ⇒ 3x = π ⇒ x = π/3 M1 A1 A1cao 3 x sin 3x = 0 3x = π or 180 x = π/3 or 105 or better (ii) When x = π/6, x sin 3x = sin 62 π π = 6 π ⇒ Q(π/6, π/6) lies on line y = x E1 1 y = 6 π or x sin 3x = x ⇒ sin 3x = 1 etc Must conclude in radians, and be exact
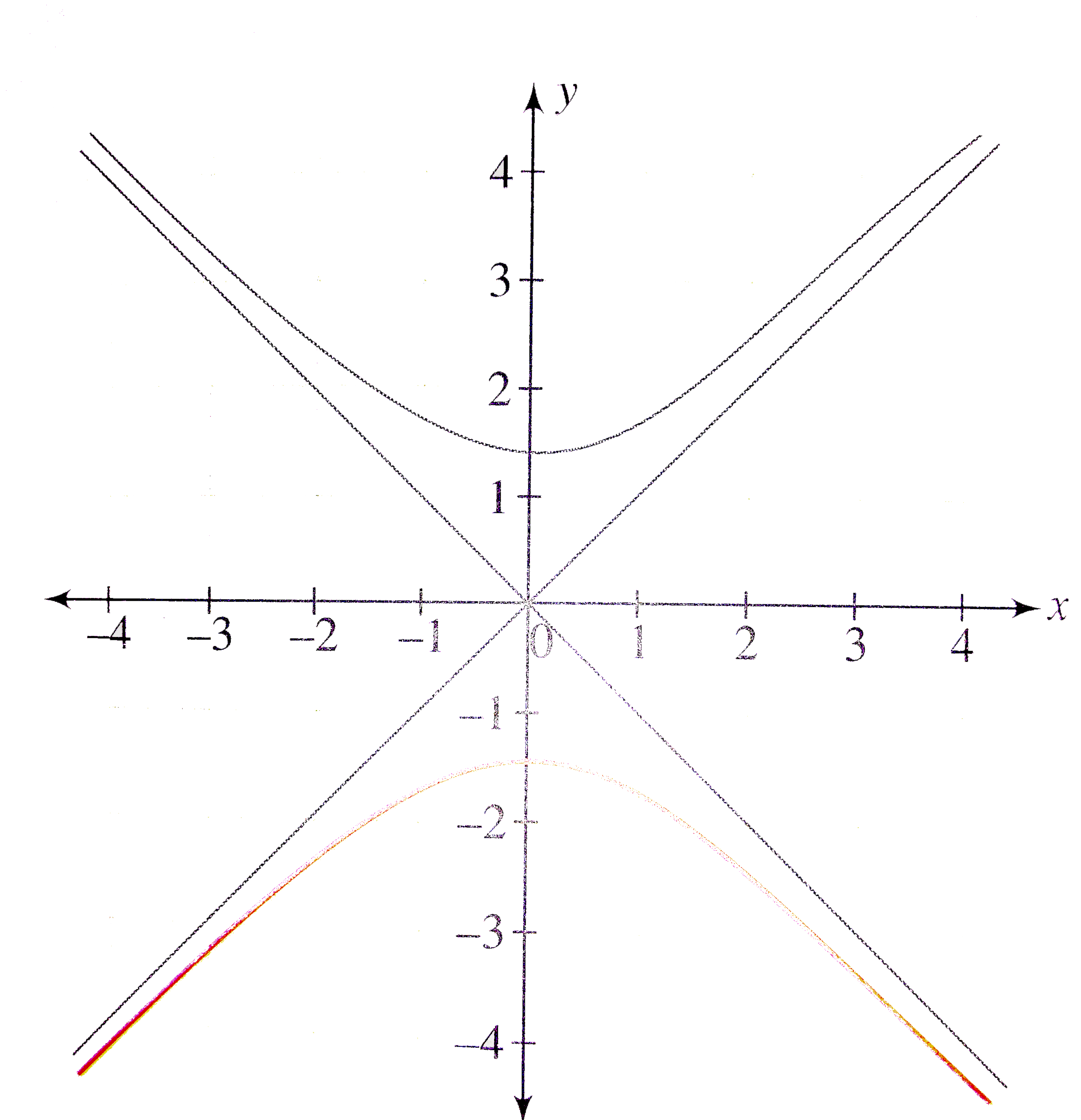


Draw The Graph Of Y Sqrt X 2 2



Graphs Of Square Root Functions Ck 12 Foundation
Learn with Tiger how to do 1/xy=1/x1/y fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, Reducing (Simplifying) Fractions Tiger Algebra SolverGraph y = square root of 1x^2 Find the domain for so that a list of values can be picked to find a list of points , which will help graphing the radical Tap for more stepsCON هر ث Submit Answer 2 2 27 3 47 3 The base of a solid is the region in the first quadrant between the graph of y = and the x – axis for 0 < x < 1
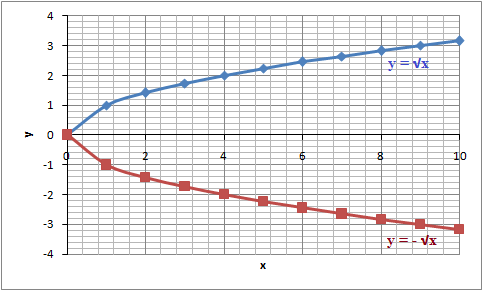


The Graph Of A Radical Function Algebra 1 Radical Expressions Mathplanet



Shifts Of Square Root Functions Read Algebra Ck 12 Foundation
View this answer The level curves of the following functions using the given window {eq}z {/eq} values {eq}1 z = 2 x y;(c) Then use technology to compute an approximation of accurate to within (d) Finally calculate the number What number does approximate?#Domain #Range #FunctionsFind the Domain and the Range of the square root function y = square root of (1 x^2)Learn more about functions here https//wwwf



Graphing Square Root Functions



Implicit Differentiation


The Inverse Cosine Function
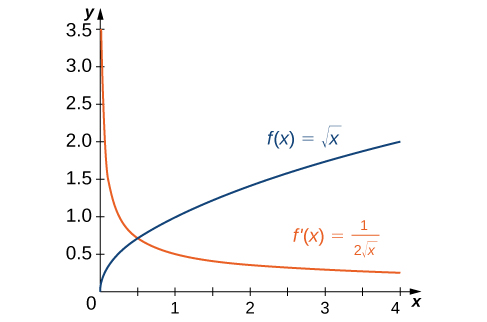


3 2 The Derivative As A Function Calculus Volume 1



Asymptote Wikipedia


Solving Equations Algebraically


Solution Test The Equation For Symmetry And Sketch Its Graph Y Sqrt 1 X 2 Thats Y Equals Negative Square Root 1 Minus X Squared


Solution How To Sketch The Graph Of Y Sqrt X 1


Square Root Graphs In Depth Expii


Use The Graph Of A Function To Graph Its Inverse College Algebra


How Do You Translate Graphs Of Square Root Functions Socratic
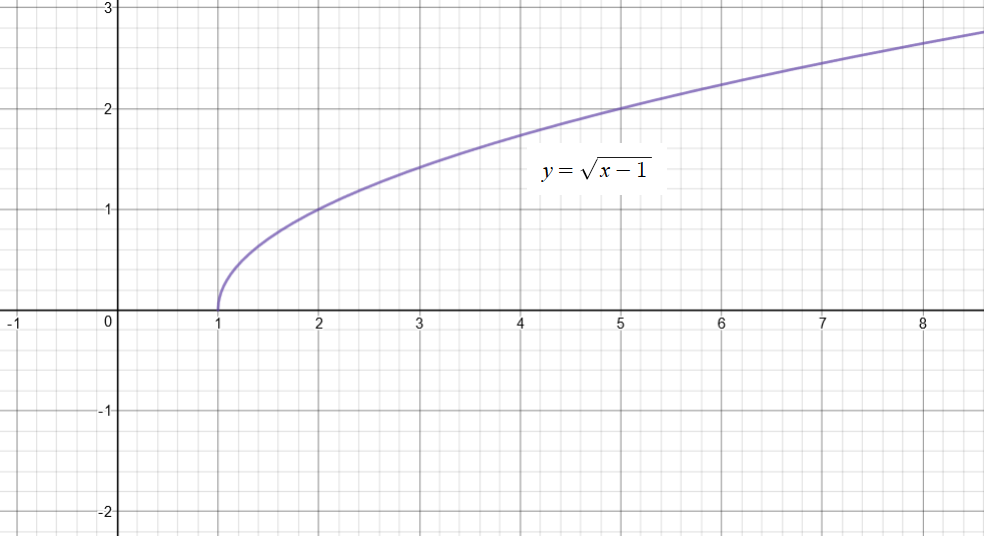


What Is The Domain And Range For F X Sqrt X 1 Socratic



Find Domain And Range Of Function Y Sqrt 1 X 2 Youtube



Graphing Square And Cube Root Functions Video Khan Academy
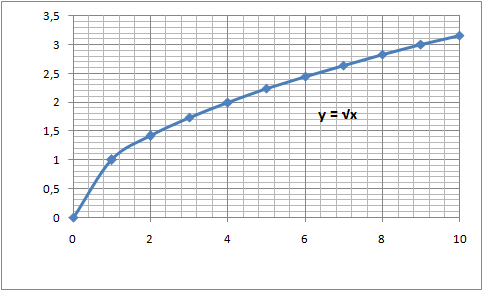


The Graph Of A Radical Function Algebra 1 Radical Expressions Mathplanet



Solved The Domain Of The Function F X Y Square Root Chegg Com



Transforming The Square Root Function Video Khan Academy
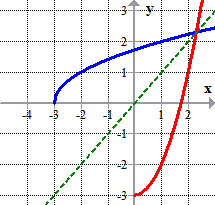


Inverse Of Square Root Function Chilimath



3d Domain Find The Domain Of Z Sqrt Y X 2 And Ln X 2 Y 2 9 Then Sketch The Domain Youtube
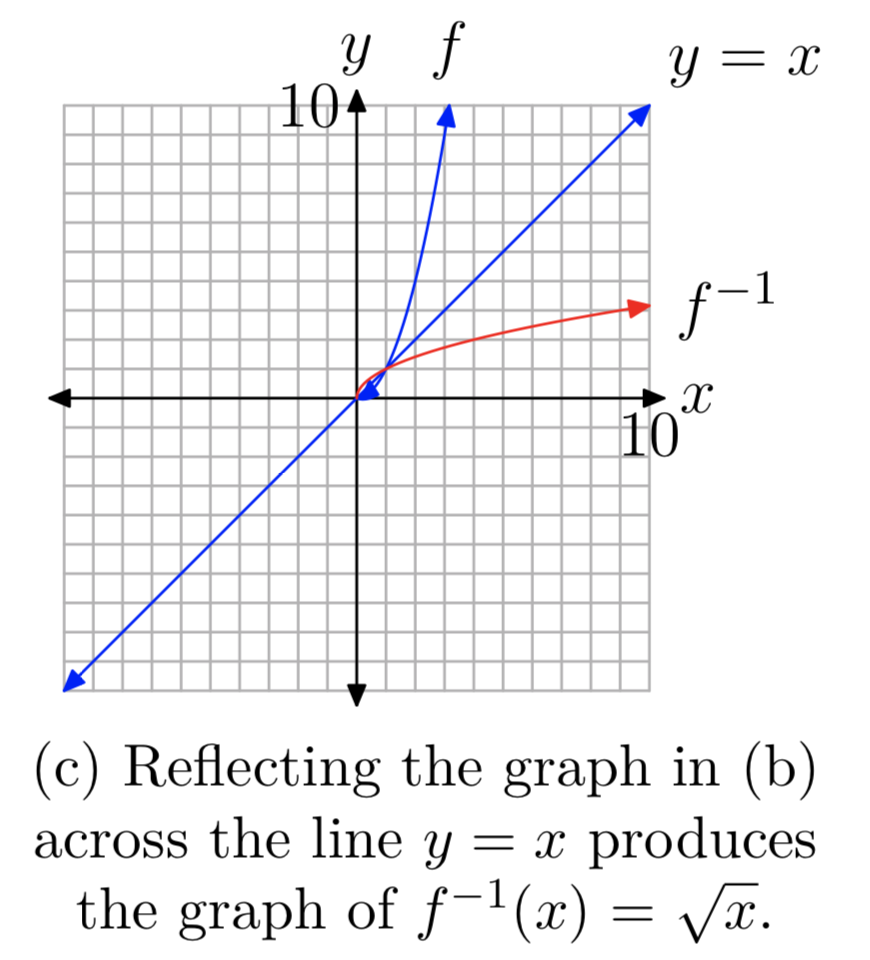


9 1 The Square Root Function Mathematics Libretexts



How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange


5 4 Prezi By Anna Two Section 54 Ppt Download



Does A Square Root Have Two Values Brilliant Math Science Wiki


Solution Use The Graph Of F X Sqrt X To Sketch The Graph Of A Y F X 1 B Y F X 3 Is There A Formula I Can Use To Come Up With The Solution I Would Show My



How To Draw Y 2 X 2


Graphing Square Root Functions



Integral Of 1 Sqrt 1 X 2 Youtube


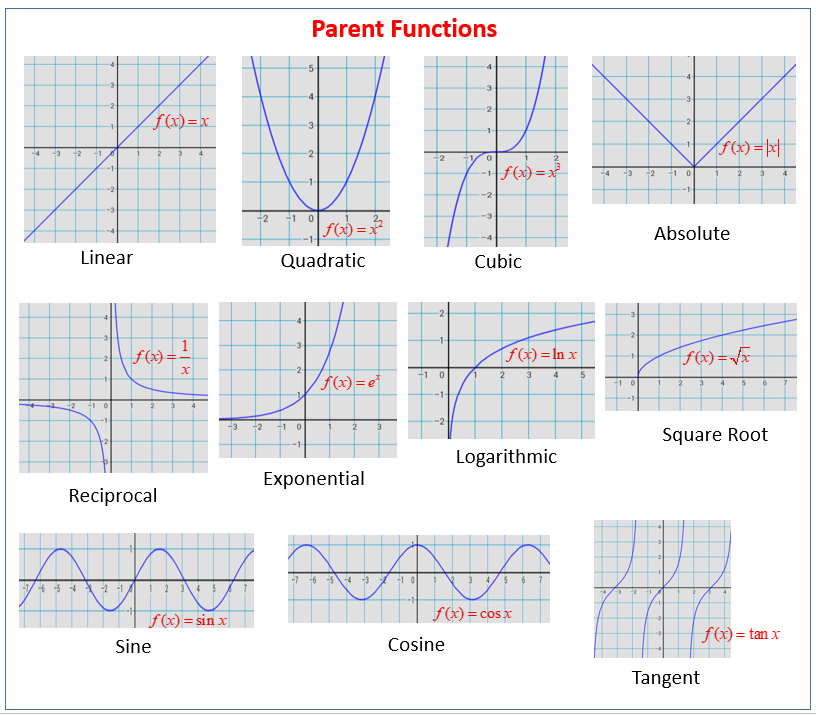
Parent Functions Types Properties Examples


Area Of A Region Bounded By Curves


Using Transformations To Graph Functions


Area Of A Region Bounded By Curves


Or Sqrt Square Root Function Librow Digital Lcd Dashboards For Cars And Boats



What Will The Graph Of Y 1 X Be Quora


Solving Equations Algebraically


Customizing Graphics


Find Range Of Square Root Functions
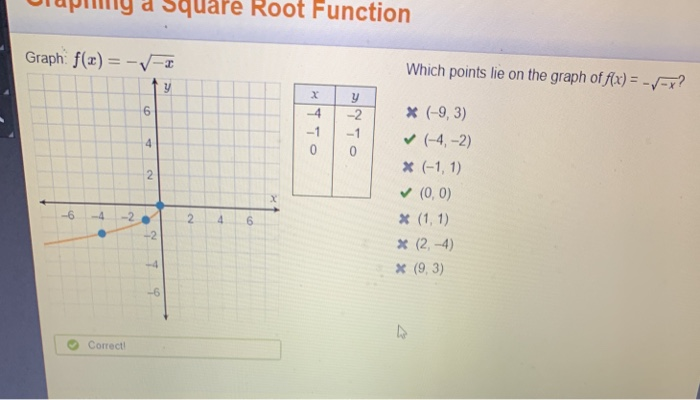


Solved A Square Root Function Graph F X V Which Poi Chegg Com
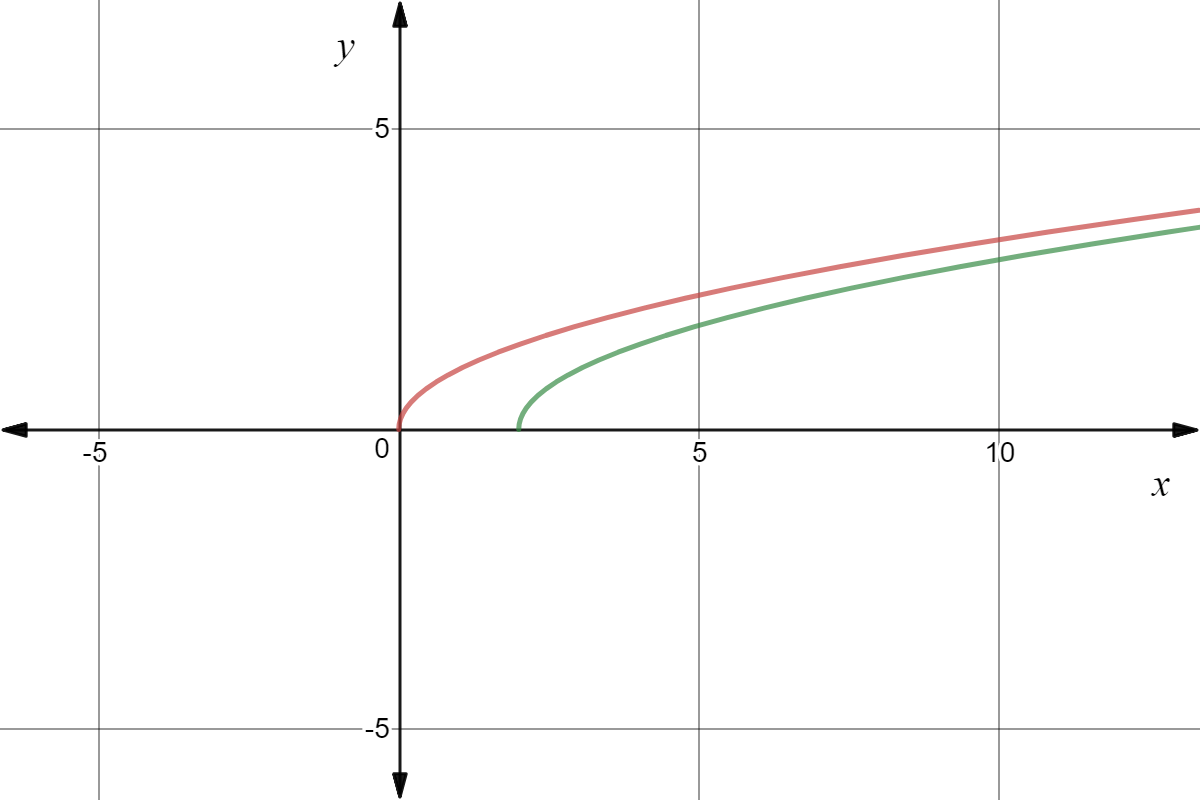


Horizontal Translation Of Square Root Graphs Expii


5 Derivative Of The Logarithmic Function


4 5 Html



1b Sketch The Graph Of The Functions F X Sqrt Of 4 X Power2 Youtube
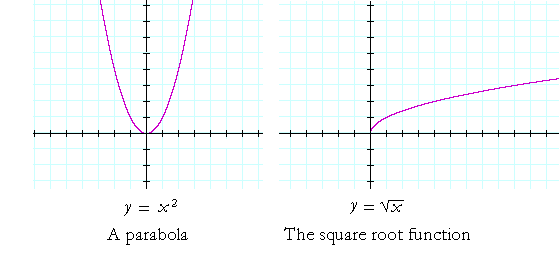


Graph Of A Parabola Topics In Precalculus


Is Y Sqrt X 2 1 A Function Quora



What Will The Graph Of Y 1 X Be Quora
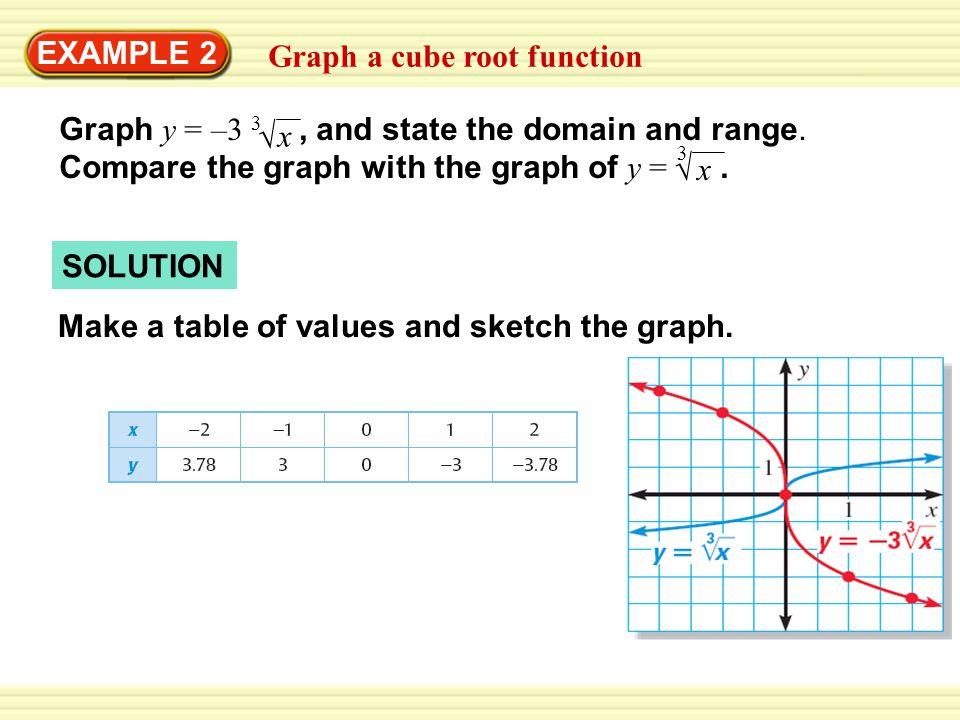


Example 1 Graph A Square Root Function Graph Y And State The Domain And Range Compare The Graph With The Graph Of Y 1 2 X X Solution Make A Table Ppt Download


The Complex Squaring Function In Polar Coordinates



Find The Domain Of F X Sqrt 1 Sqrt 1 Sqrt 1 X 2


What Is The Graph Of X 2 Y 3 X 2 2 1 Quora
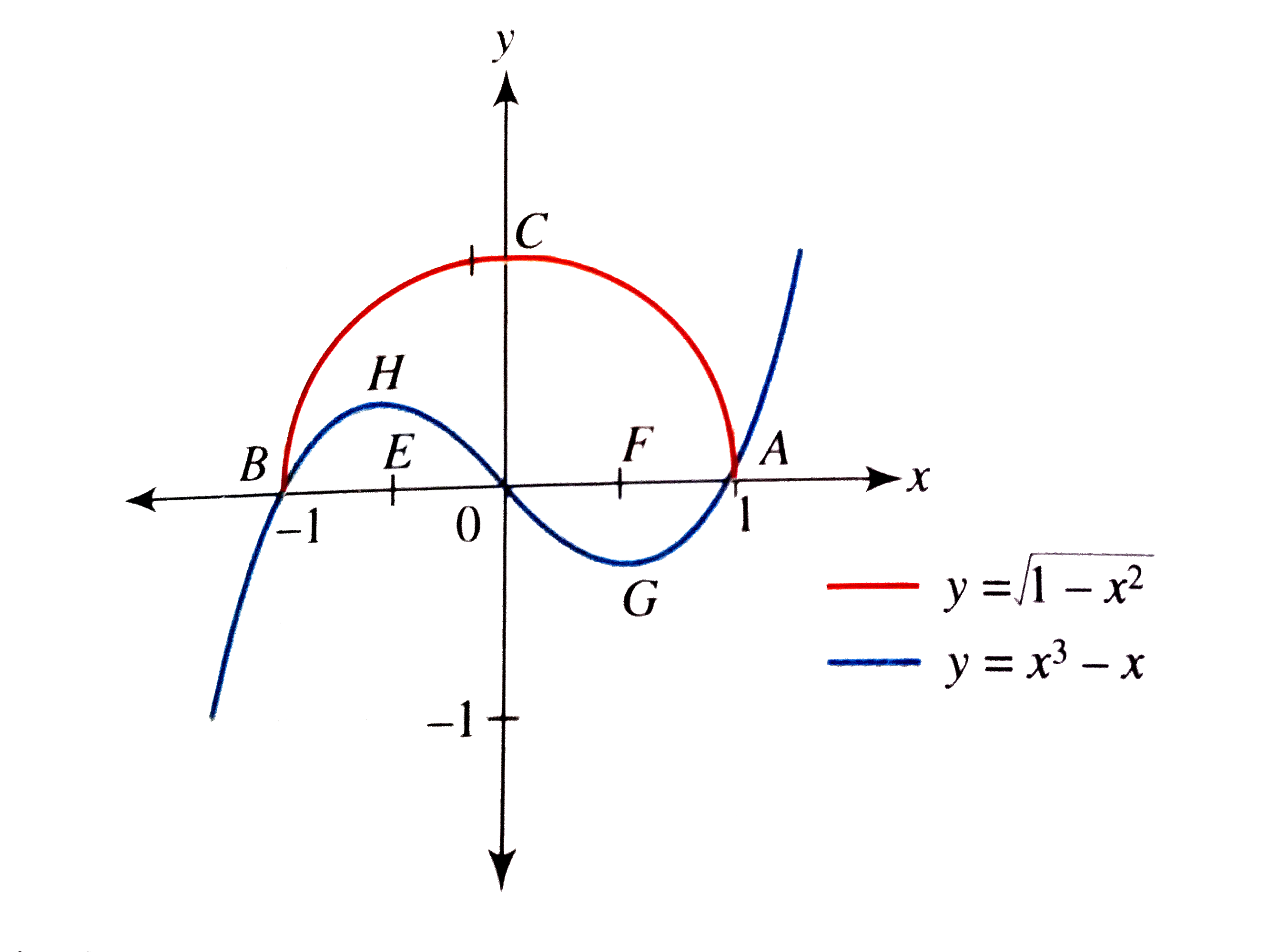


Find The Area Bounded By The Curves Y Sqrt 1 X 2 And Y X 3


Graphing Types Of Functions


Graphing The Basic Functions



Shifts Of Square Root Functions Read Algebra Ck 12 Foundation


Content Finding Domains And Ranges
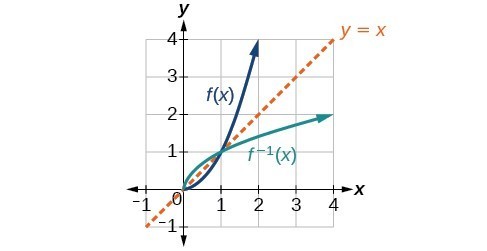


Use The Graph Of A Function To Graph Its Inverse College Algebra
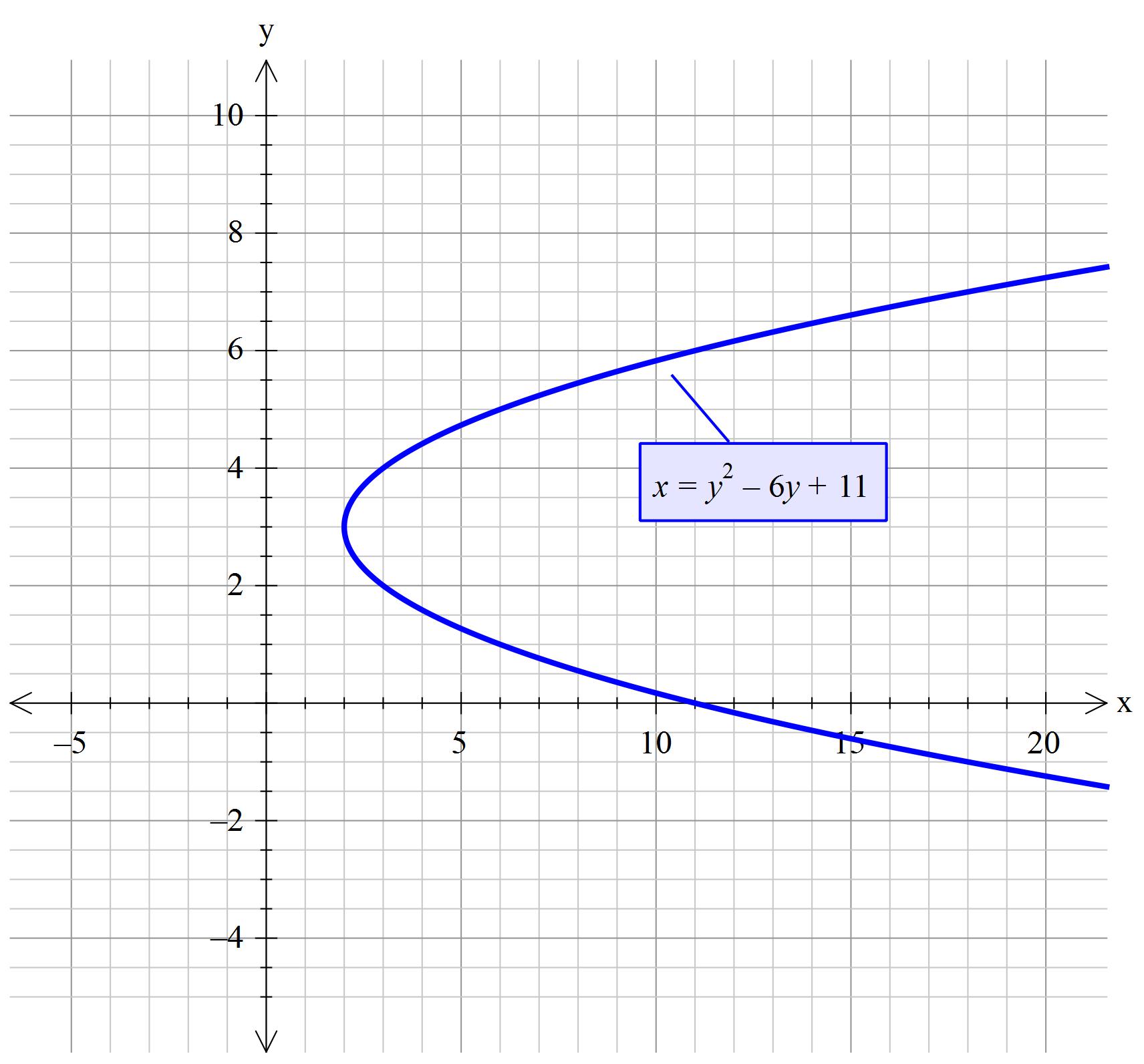


How Do You Graph Y Sqrt X 2 3 Socratic


Graphing Square Root Functions



Transformations Of The 1 X Function Video Lesson Transcript Study Com



Horizontal Line Test
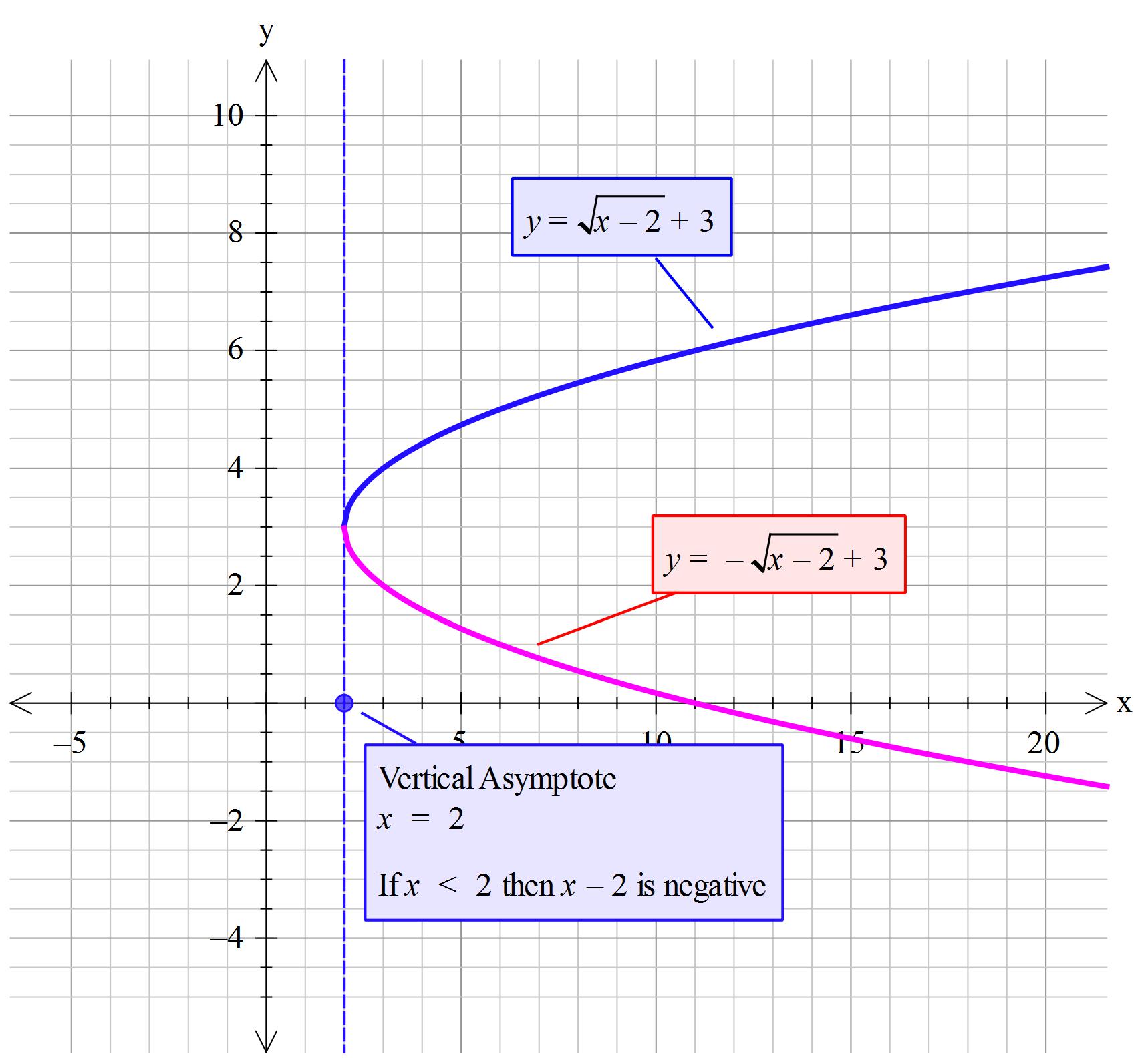


How Do You Graph Y Sqrt X 2 3 Socratic
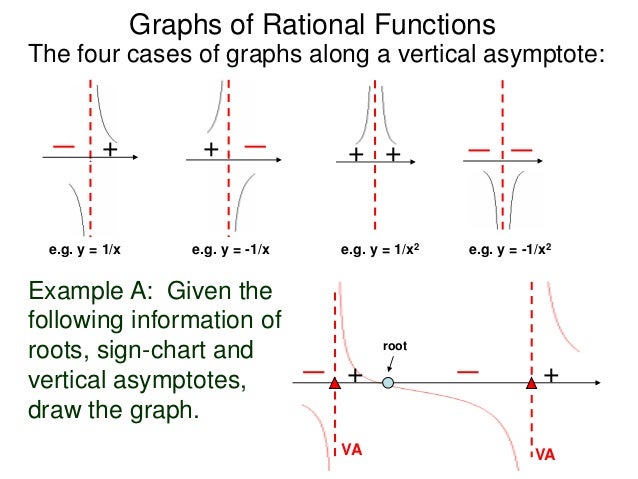


2 9 Graphs Of Factorable Rational Functions T



Solved For F X Y 1 Square Root 9 X 2 Y 2 Find Th Chegg Com
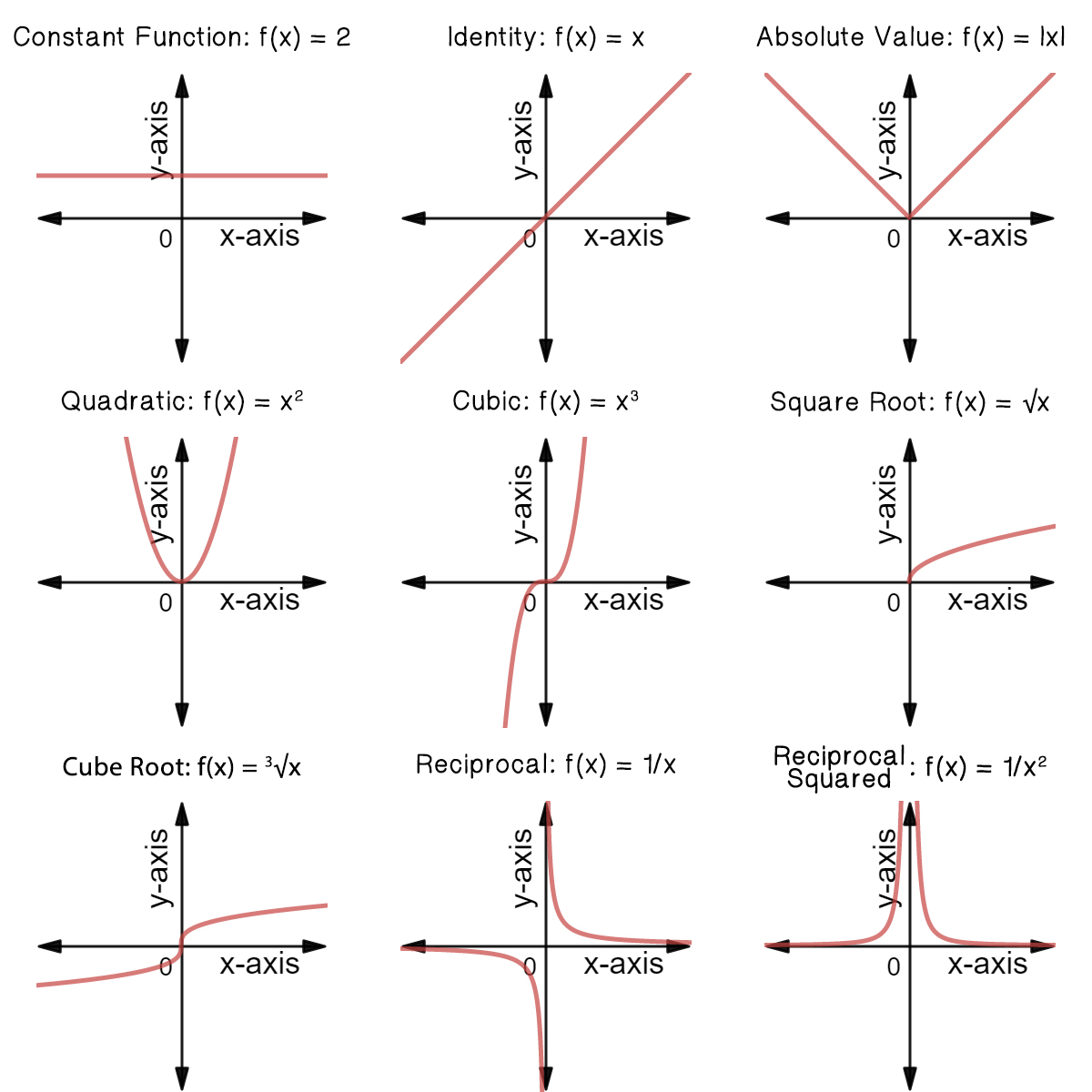


Classifying Common Functions Expii


Graphs In Physics



How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange


Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver


Graphing Square Root Functions


Root Functions



Find The Centroid Of The Region Bounded By The Curve Y Sqrt 1 X 2 And The Axes Where X And Y Are Greater Than Or Equal To Zero Study Com


Graphs Root
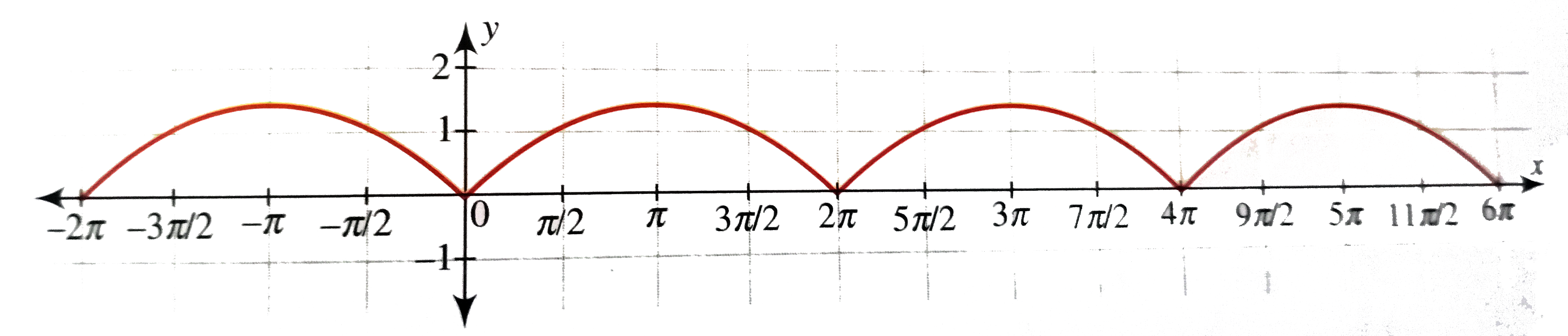


Draw The Graph Of Y F X Sqrt 1 Cosx
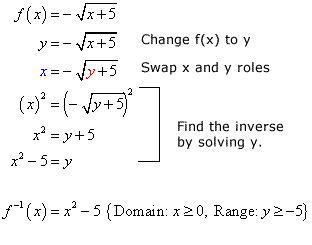


Inverse Of Square Root Function Chilimath
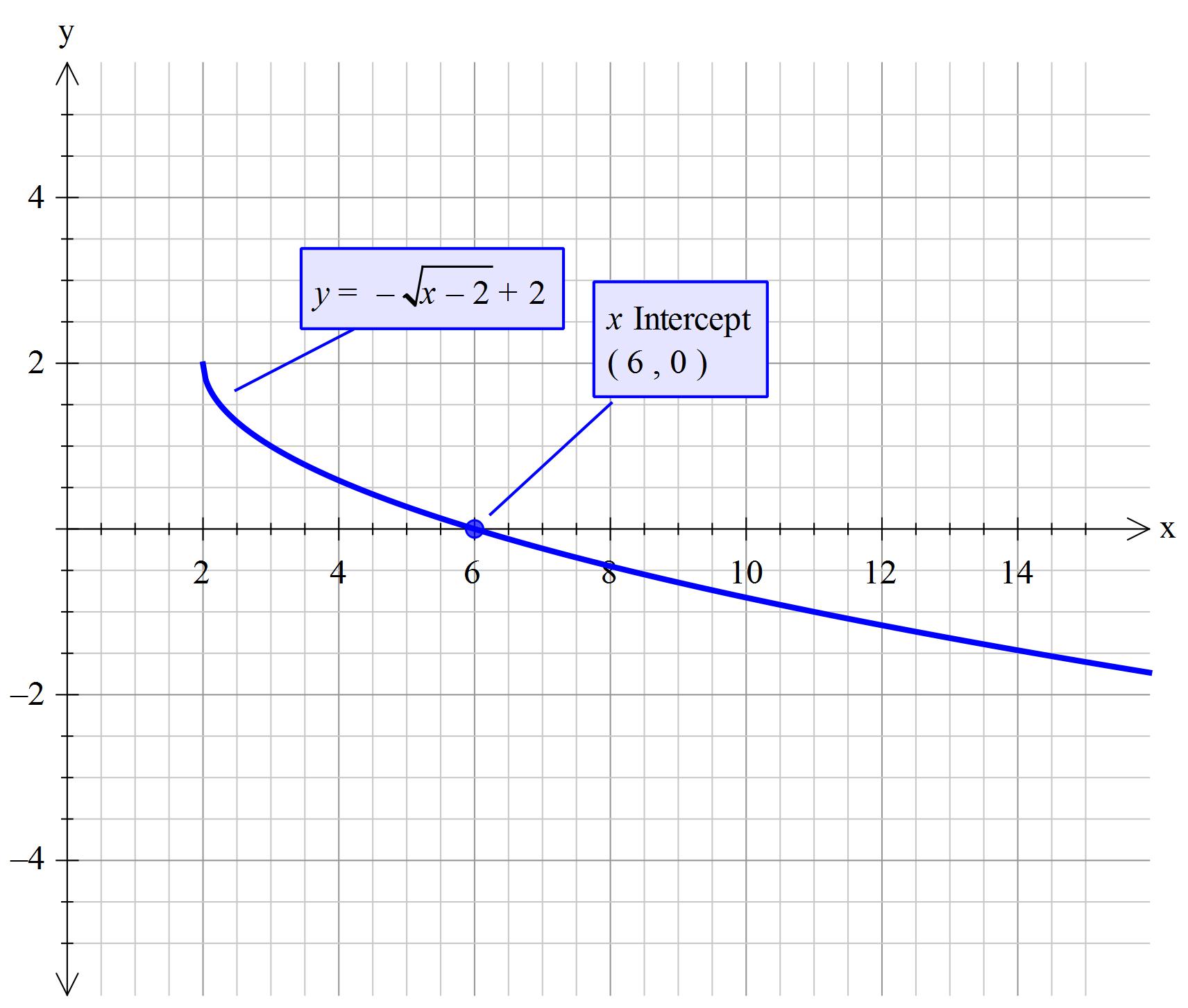


How Do You Graph Y Sqrt X 2 2 Socratic
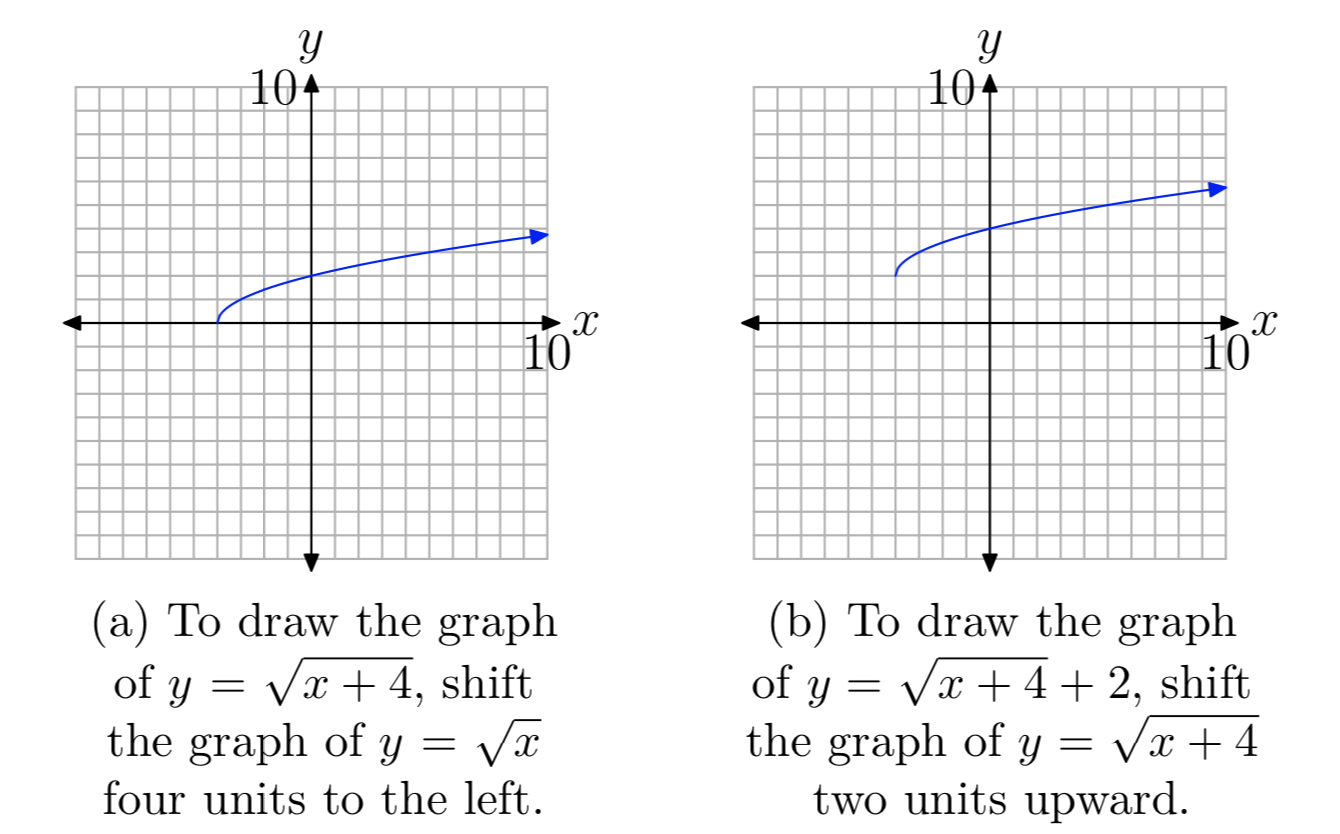


9 1 The Square Root Function Mathematics Libretexts
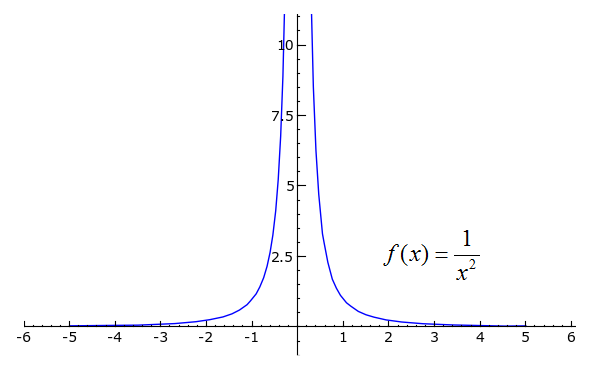


Sage Calculus Tutorial Differentiability
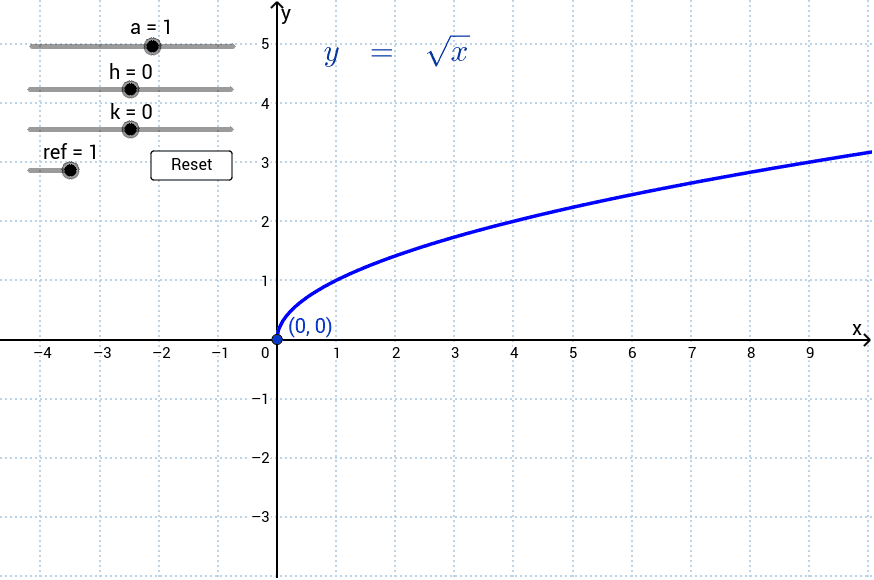


Transformations Of The Graph Y Sqrt X Geogebra



Graphing Square Root Functions



0 件のコメント:
コメントを投稿