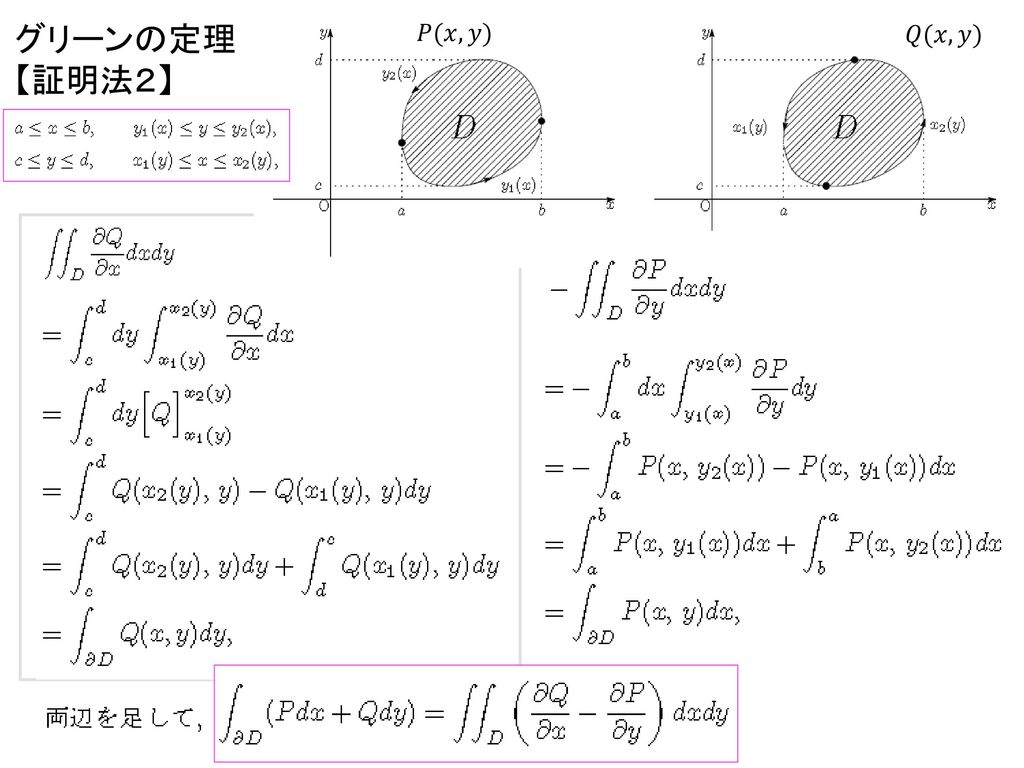
グリーンの定理 単純閉曲線C(= @D) に囲まれた領域D について ∫ @D Pdx Qdy = ∫∫ D (@Q @x @P @y) dxdy 解説(高校数学との比較) 積分が1次元高い Version Pdx Qdy !に対し、ガウスの発散定理を用いて ³³ S F dS * * を求めよ。 問題3 平面に関するグリーンの定理を用いて、曲線C: x2 y 2 4 に関して I x y³ dx x y dy C 2 3 を求めよ。 問題4 F i j k * * * * x y z のとき、 ³³ S FndS ** を ガウスの発散定理を用いて求めよ。 ここで、S はグリーンの公式 領域D を細かい正方形に分割して、縁に沿った回転量を足 し合わせると、隣り合った正方形の境界上は打ち消し合っ て、領域の縁に沿った和だけが残る。 分割を細かくしてh → 0 の極限を取ると以下のグリーンの定 理が得られる:Z C F· dr= ZZ D ∂F2 ∂x

グリーンの定理
ガウスグリーンの定理
ガウスグリーンの定理-これをグリーンの第一公式という. また, ( )= 2 ( )= 2 両式を引き算して, ( – )= 2 – 2 これにガウスの定理を適用すると (φ∇ψ – ψ∇φ ) ⋅ dS S = φ∇2ψ – ψ∇2φ dv V これをグリーンの第二公式というグリーンの定理は,1変数の関数の部分積分の公式に似ている.部分積分は,関数の積の微分 ( 31) から導ける.両辺を積分し,順番を入れ替えると ( 32) となり,部分積分の公式が導かれた. このように単純な方法で導かれる部分積分の公式は,本当に便利




ガウスグリーンの定理をわかりやすく解説 大学生 専門学校生 社会人 数学のノート Clear
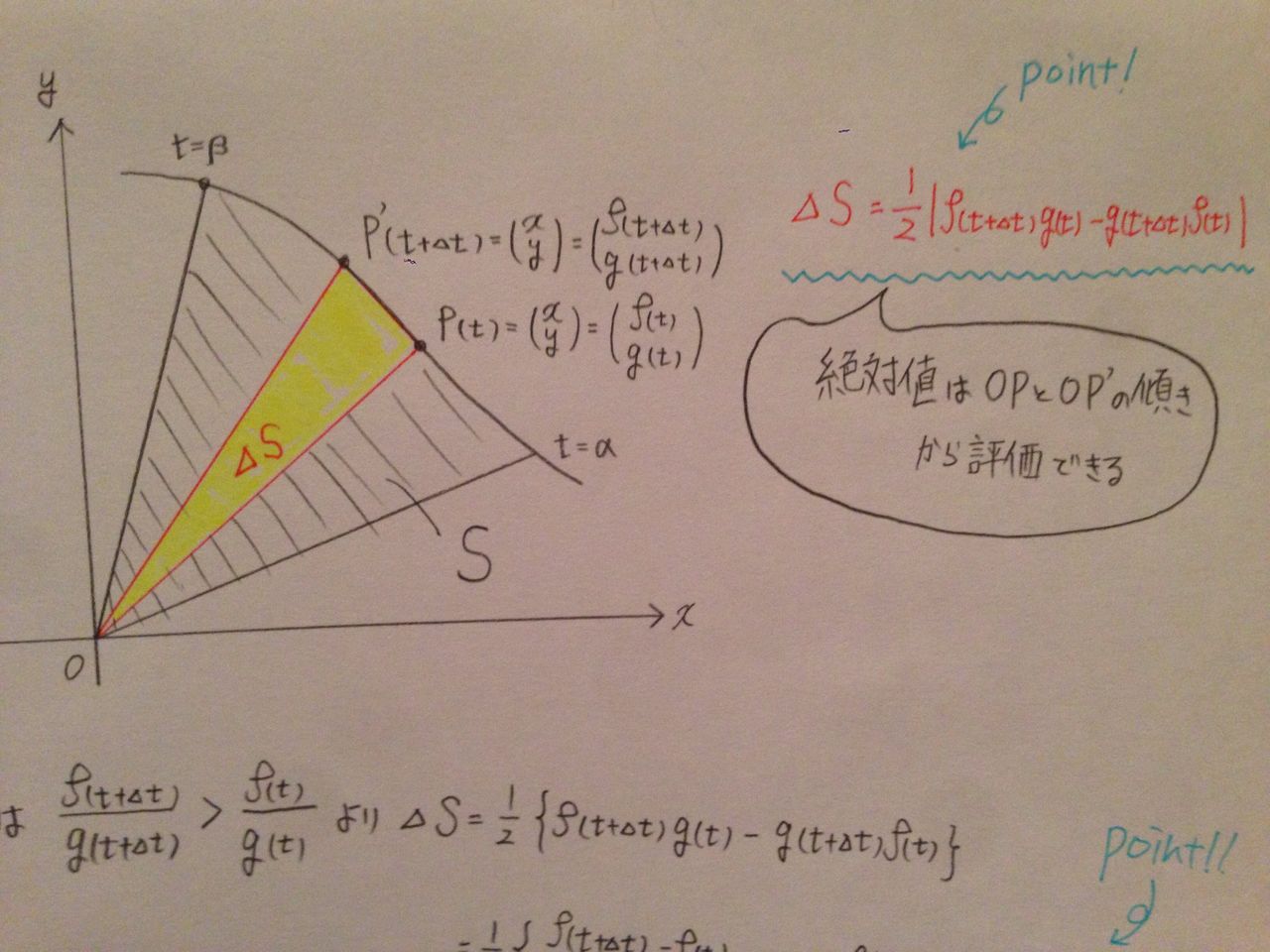
4 ガウス・グリーンの公式 定理44 Dを有限個のなめらかな曲線で囲まれる有界な閉集合とする. 境界を∂Dと書く.f,gがDでC1級の関数ならば ∫ ∂D f(x,y)dxg(x,y)dy= ∫ D (∂g ∂x ∂f ∂y) dxdy が成り立つ.ただし,∂Dの向きは進行方向左側にDの内部を見るようガウスグリーンの定理 Geogebra 面積 17 グリーンの公式の系のまとめ 怜悧玲瓏 高校数学を天空から俯瞰する 平面のグリーンの定理 物理のかぎしっぽGaussGreenの定理の証明 Step 1 符号つき面積 Oを原点とする座標平面上の OABに対し、原点から見てO(0, 0), A(a, b), B(c, d)が「左回りのとき正、右回りのとき負」・・・(*)となるような OABの面積を「符号つき面積」とよぶ。
Dec 22, 19 · まずは グリーンの定理 からはじめ、次回から ガウスの発散定理 と ストークスの定理 を示していきます。 線積分や面積分、体積積分を書き換えることができるこれらの定理は、電磁気学をはじめ様々な分野で活用することになりますので、証明の流れや1 .ガウスの定理 (発散定理) ある状況下では,体積積分を面積分に置き換えることができます。 ガウスの定理 3次元ユークリッド空間の有界な領域をV,その境界面を S とする。 この閉領域で定義されたベクトル関数 A (x,y,z) について, ∇・ A dV= A ・ nグリーンの定理ガウスの定理 超関数の世界 第 章 解析学の舞台・・・関数の近似関数空間 関数を近似する フーリエ級数展開 複素数とオイラーの公式コーシーの定理 フーリエ変換 ソボレフ空間 関数の近似の道具軟化子 第
Sep 02, · グリーンの定理(2次元) グリーンの定理(3次元)を、ガウスの定理を用いて証明しました。 次は、グリーンの定理(2次元)を解説していきます。 グ リ ー ン の 定 理 ( 次 元 ) グ リ ー ン の 定 理 ( 2 次 元 )• ガウス・グリーンの定理 • 偏微分方程式の数値解法(変分法)ガウス生誕の地(Brunswick)に建つガウスの像 面積分⇔体積分 ガウスの定理 ガウスの定理の(直感的)導出 P Q R 体積 の微小直方体を考える。 この微小直方体の表面 上での面積分: を計算する。 図21 積分面(ガウス面) ここで、n は積分面の単位法線




ガウスの法則 例題




デザルグの定理 メネラウスの定理 応用問題 勉強 Youtube スタディチューブ
グリーンの定理は領域d の境界線上の線積分が領域d の面積分(2重積分)に変換できる(逆も同 様)ことを示す有名な定理です。 11 グリーンの定理(その1)-線積分と2重積分-グリーンの定理の別証 {1{ 定理 Dをxy平面の有界な領域で,その境界Cは互いに交わら ない有限個の区分的にC1 級の単一閉曲線からなっているとする そのときDを含む開集合でC1 級の関数f(x;y);g(x;y)に対して ∫∫ D (@g @x @f @y) dxdy= ∫ C fdxgdy が成り立つ ここで, CにはDに対して正の向きをつけて1.グリーンの定理 が成り立つ。 これは次の個別に成り立つ2つの積分の和である。 とし,積分範囲は右図のように底面が xy 平面内にある領域 D (この周囲を C とする)で高さが1の鉛直に立つ柱とします。 そしてこの柱の 一方,ガウスの定理の右辺 (面積



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配
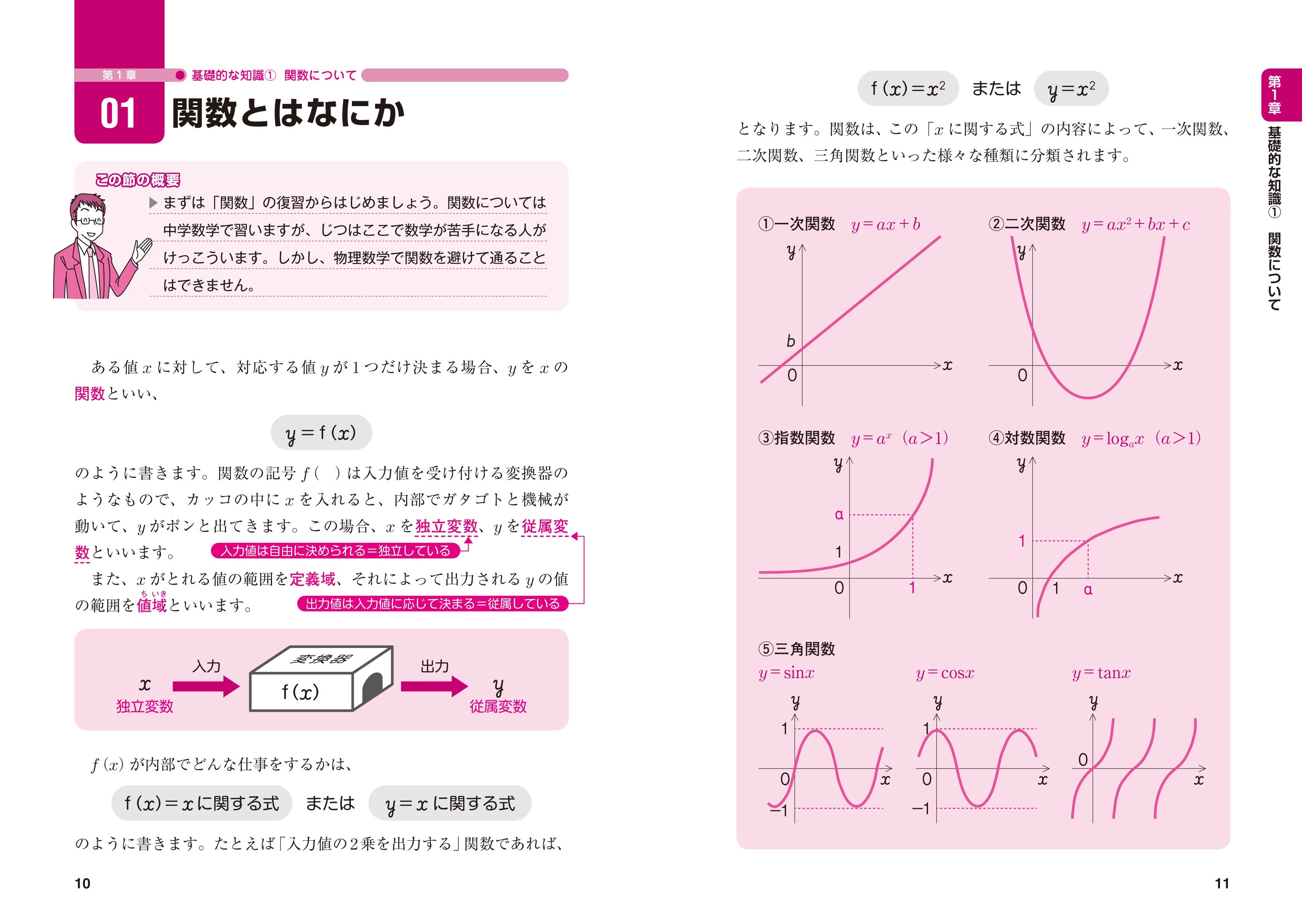



高校レベルからはじめる やさしくわかる物理学のための数学 ナツメ社
これをグリーンの定理といいます。線積分と2重積分を変換する定理です。 とこんなことである。それで私には何だかよくわからないまま通過してしまったものである。 私の頭には、 ・ 何故変換定理が必要なのNov 19, 19 · 有限要素法を学ぶときに出てきました。自分に対して分かりやすく書いたものは、恐らく他人にもわかりやすくなるだろうと思ってます。 学部時代にテストで出たのにさっぱり忘れた内容でした! キーワード 有限要素法,変分法,計算力学,数値解析,グリーンの定理,ガウスグリーンの公式この記事では, ガウスの発散定理から,グリーンの定理と呼ばれる定理を二つ導きます.既出の 平面のグリーンの定理と区別するため,これらを グリーンの第一定理, グリーンの第二定理と呼ぶことにします.グリーンの第一・第二定理は,ガウスの発散定理から導かれる派生的な定理ですが,ポテンシャル理論で重要なため,それなりに有名な定理です




テラスハウス ガウス グリーンの定理 理系 落ちこぼれkの東大受験日記




ガウス グリーンの定理 高校生ver Youtube
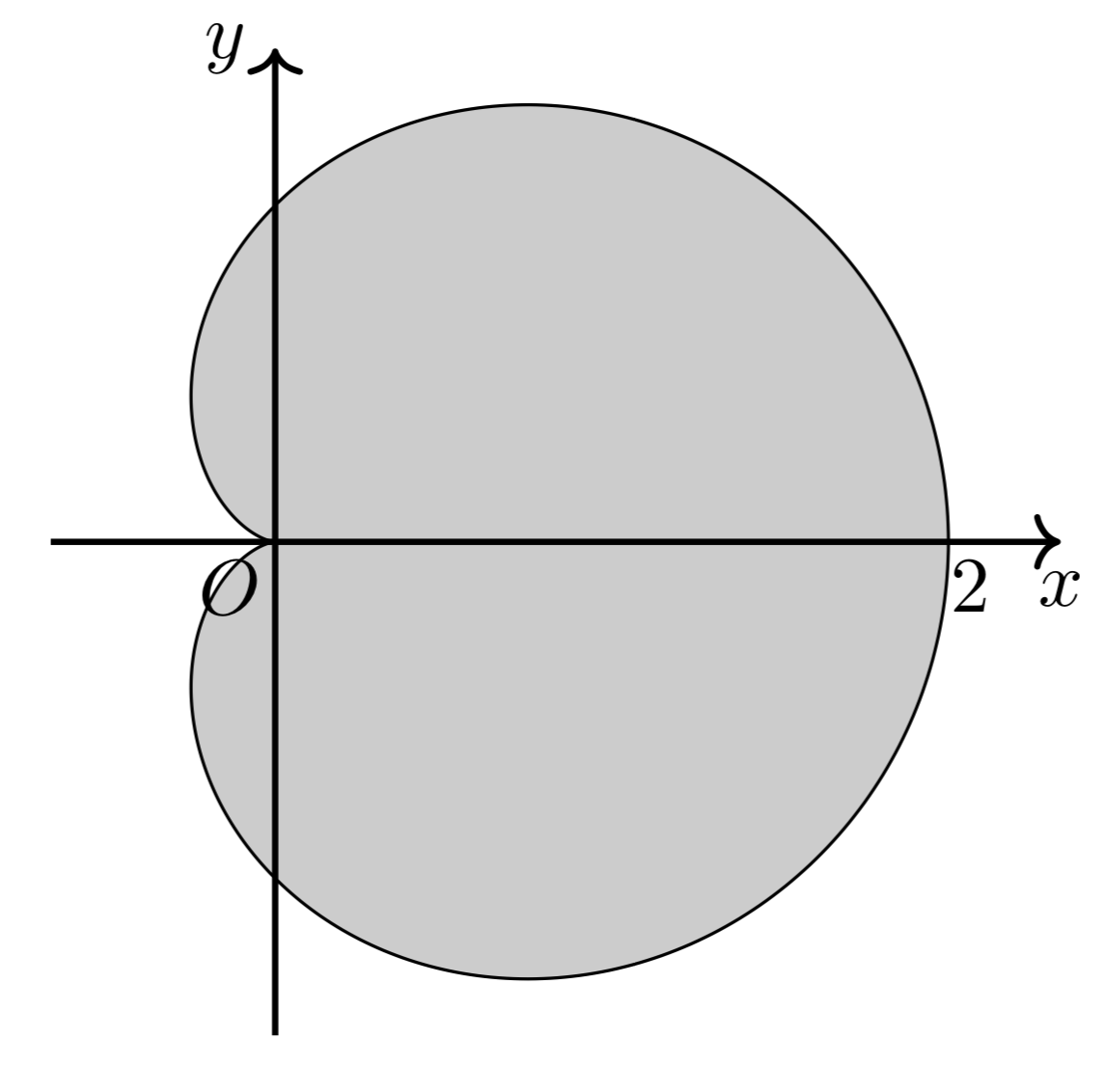
Aug 29, 18 · ガウスグリーンの定理 この定理を使うと、円の面積を簡単に求めることができる。が成り立つ、という結果がグリーンの定理であった。前回の講義ではグリーンの定理 から、平面上のガウスの発散定理が成り立つことを示した。 定理111 (平面におけるガウスの発散定理)平面において、c を自己交差しないグリーンとは誰か? 大学に入学して理工系の勉強を始めると誰でも, ガウスの定理とグリーンの定理という ふたつの積分定理を教えられることになる ガウス( Carl Friedrich Gauss ) は大数学者であり, 良く知られている人物である




ガウスグリーンの定理 Geogebra
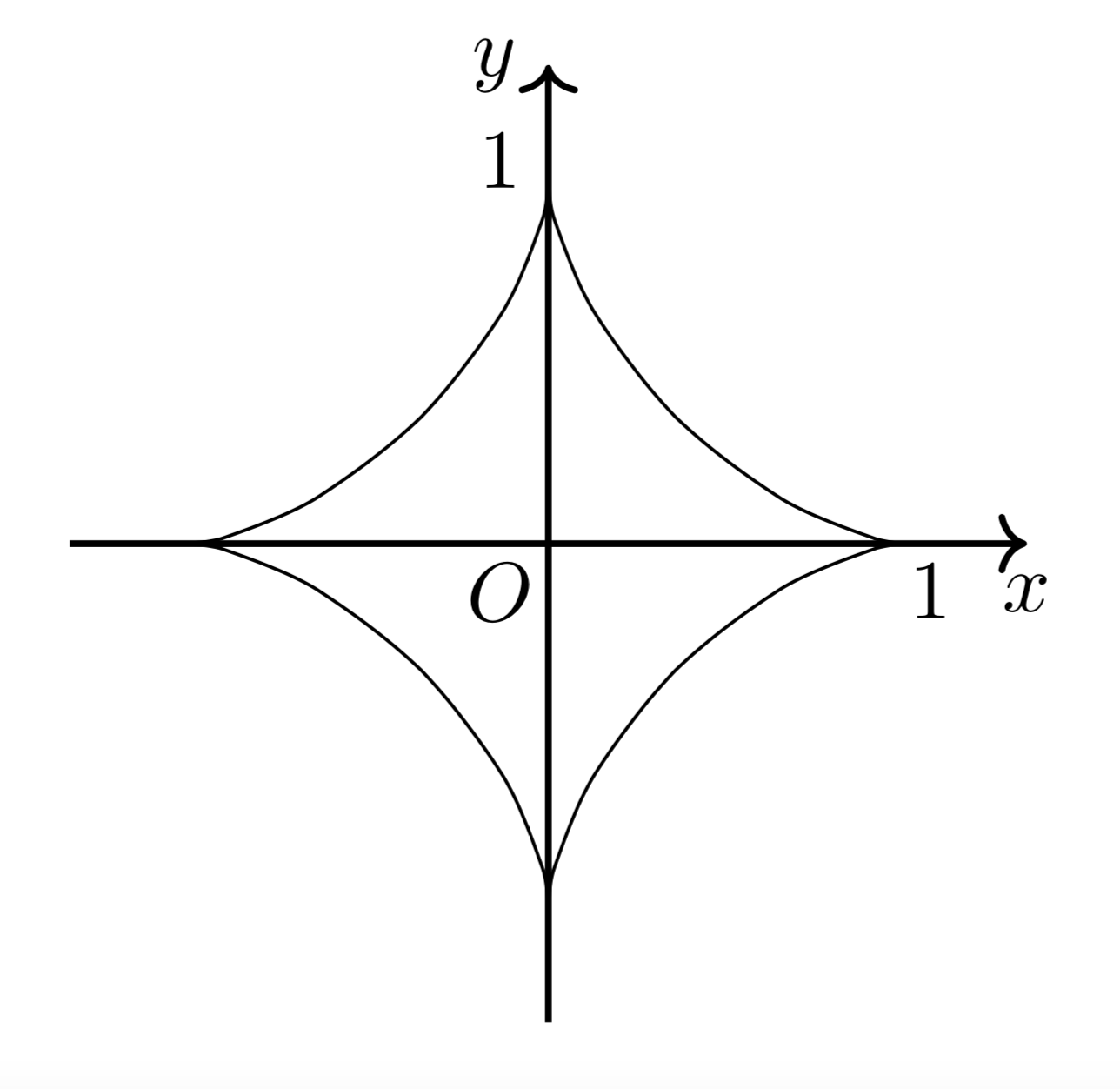



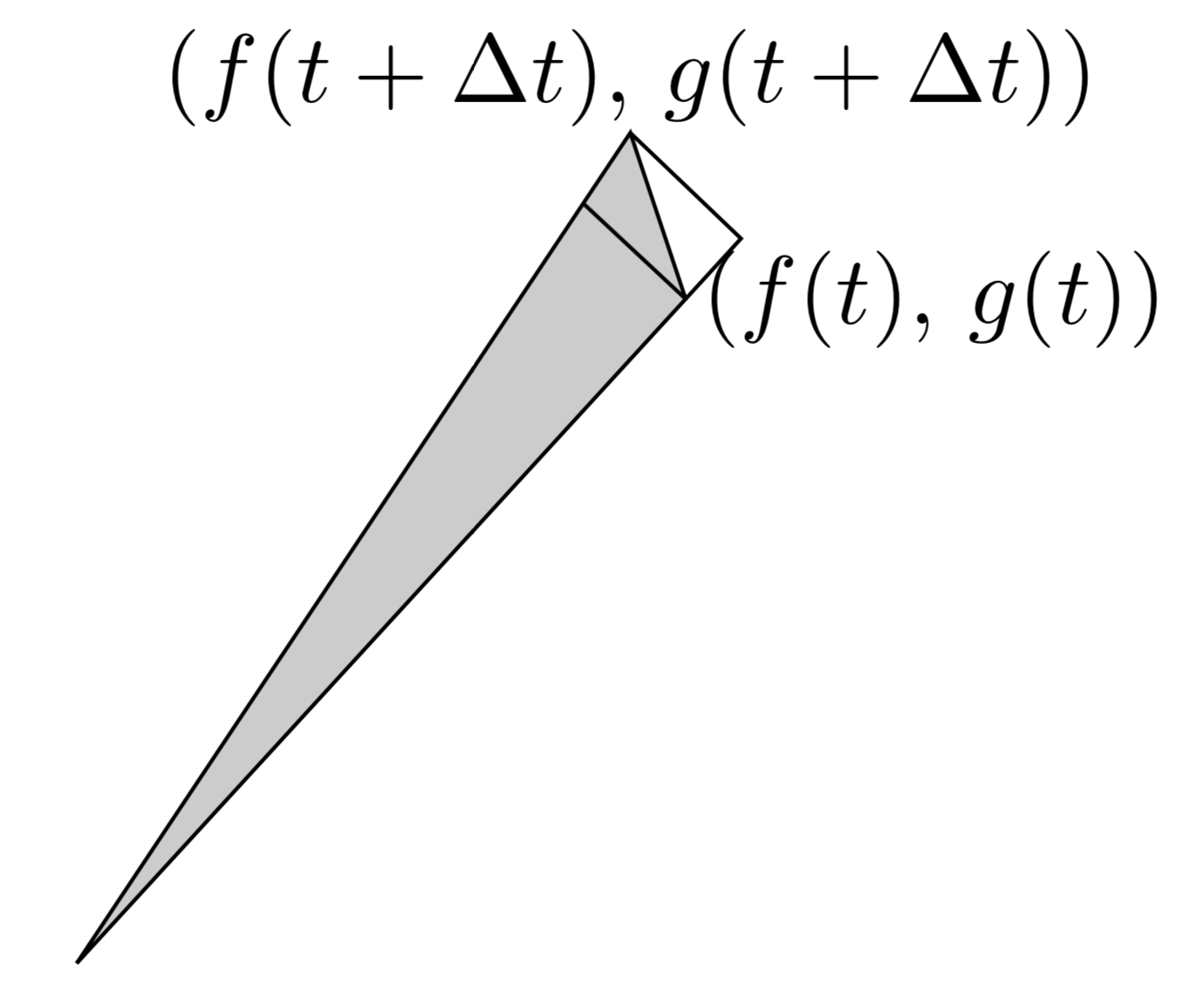
媒介変数表示されたグラフの面積の求め方を例題付きで解説 検算に使える定理も教えます 東大医学部生の相談室
Sep 11, · ガウスグリーンの定理は大学入試の記述式の入試で使っていいのですか? ん~‥記述式で、"ガウスグリーンの定理より"って書いたら、多分NGだと思います。グリーン グリーンの定理にその名をとどめるグリーン は,英国ノッティンガムの裕福なパン屋に生まれました.家業は順調で,一家は経済的には不自由なく暮らしましたが, 年には内乱のため食料の欠乏した民衆に家を襲撃されるという,イギリス版米騒動のような被害にも遭っています.グリーンの父が建設した粉挽き用の風車は現在もノッティンガムにあるそう単なるベクトルの1定理だと思いきや、微分積分学の基本定理の一般化だったでござる。 ガウスの定理の証明、ストークスの定理の証明 追うのがキツい。証明の概略でお茶を濁している本も多い。 グリーンの定理 ストークスの定理の特殊な場合。



Applied Mathematics A



オンライン教育コンテンツ 東京大学 国際工学教育推進機構 工学教育部門
よく間違える例) 13P;QはDの境界、内部ともにC1級である。そうでない場合、グ リーンの定理は成り立たない Cを単位円に反時計回りに向き付けしたものとする I= ∫ C y x2 y2 dx x x2 y2 dy を求める。 @ @y (y x2 y2 @x (x x2 y2 x2 y2 (x2 y2)2なので、形式的にグリーンの定理を用いるとI=Jun 08, 19 · 証明 ガウスの発散定理において、 ψ ∇ ϕ \psi\nabla\phi ψ∇ϕ と置いたものがグリーンの定理です。 発散定理より ∫ S n ⋅ ( ψ ∇ ϕ) d S = ∫ V d i v ( ψ ∇ ϕ) d v \displaystyle\int_ {S}\boldsymbol {n}\cdot (\psi\nabla\phi)dS=\displaystyle\int_ {V}\mathrm {div} (\psi\nabla\phi)dv ∫212 グリーンの定理 • K氏:次に、グリーンの定理だが、これはガウスの定理の表面積分と体積積分の関係を変形した ものなんだ。閉曲面S で囲まれた領域V において、2つの異なるスカラ関数u、v に対し Z V (u∇2v ∇u·∇v)dV =Z S u ∂v ∂n dS = Z S un·∇vdS (12) Z V (u∇2v −v∇2u)dV =




ガウス グリーンの定理 例題 Youtube




東大数学
グリーンの定理、次に出てくるストークスの定理は・・・ 周辺の状態から、内部の状態を見る式 というのだ。 確かにある領域を大回りして変化がゼロの場合、内部の微小領域でも 同じ事が起こっている。Jan 02, 19 · ガウスグリーンの定理の証明 ガウスグリーンの定理は高校数学では習わないので、答案に使うのは極力避けておくべきです。どうしても使わなければならない場合には証明をしてから使うのが良いでしょう。証明は以下のようになります。(@Q @x @P @y) dx ^dy 微分 正式名称は 外微分 d(Pdx Qdy) @D D 境界




ガウスの発散定理 微小要素のイメージから分かりやすく証明 スモビュ




仮面ライダービルド 数式 新オープニングの最後に流れる数式解説まとめ Fallen Physicist Rising Engineer
第13 回:グリーン、ガウス、ストークスの定理 マクスウェルの方程式を解くためにある UP が遅れて大変申し訳ありません.予習頑張ってください.グリーンの定理(グリーンのていり、英 Green's theorem)は、ベクトル解析の定理である 。イギリスの物理学者ジョージ・グリーンが導出した。2 つの異なる定理がそれぞれグリーンの定理と呼ばれる。詳細は以下に記す。同様に , および とおき, 得られた3式を辺々加えればガウスの定理が得られる 逆に ガウスの定理からグリーンの公式を導くには, ベクトル値関数として をとる このとき だからグリーンの公式が出てくる ガウスは19世紀の数学において他を寄せ付けないく らいの業績をあげた人物であるが, Cross 3 によれば, 彼が見いだしたものは ( 4 )の特殊な ものでしかなかったと



18年度後期 数学b 電気電子
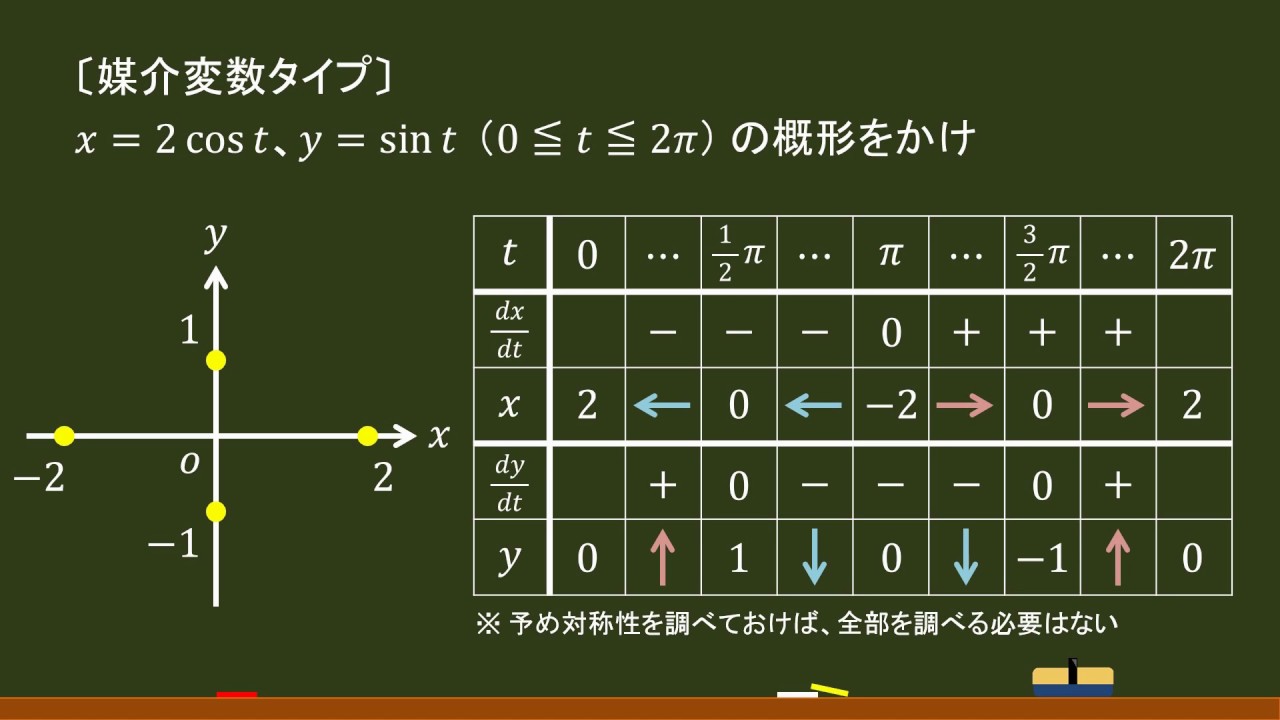



媒介 変数 積分 積分の応用の問題
を得る。これがグリーンの定理である。 いま、ポアソン方程式に境界条件を満たす解が2つあったとする。それらをφ1 、φ2 とし、 その差をψとする。即ち、 ψ=φ1 −φ2 とする。φ1 、φ2 は境界条件を満たすので、境界面Sでψ=0となる。従って、グリーンの




Wo10 号 物理量計算方法 数値解析方法 物理量計算プログラム 数値解析プログラム 物理量計算装置及び数値解析装置 Astamuse



微分積分 16




完全微分方程式とド ラームコホモロジー Tsujimotterのノートブック




Paypayフリマ ベクトル解析から流体へ 坂田高夫 柴田良弘 著 日本評論社




ガウスの発散定理 微小要素のイメージから分かりやすく証明 スモビュ



Powerpoint プレゼンテーション Pdf Free Download




ガウスグリーンの定理をわかりやすく解説 大学生 専門学校生 社会人 数学のノート Clear




講師 幹 浩文 A314 Ta 西方良太 m1 A305 Ppt Download



Powerpoint プレゼンテーション Pdf Free Download




ベクトル解析 Speaker Deck
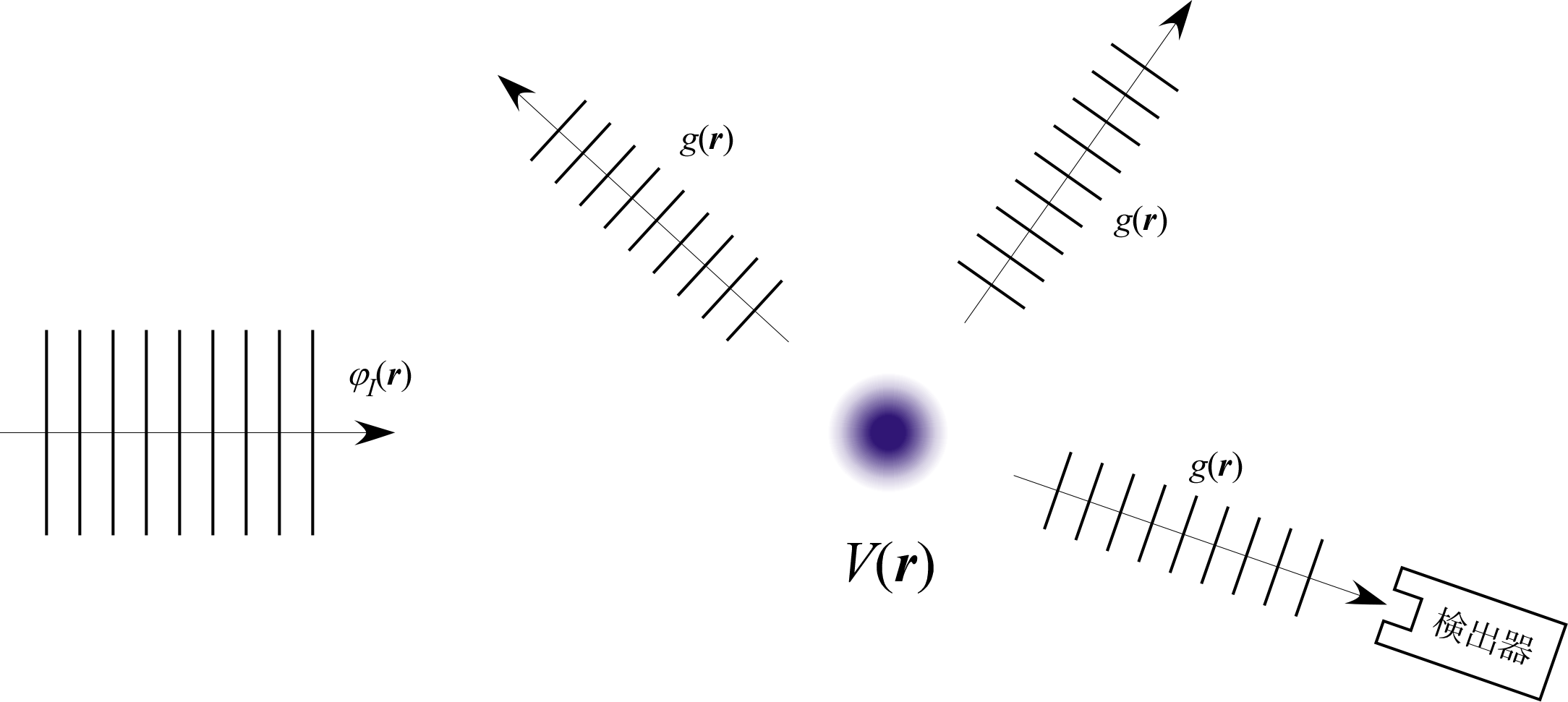



量子力学 三次元空間での散乱現象 武内 筑波大




ガウスの発散定理 微小要素のイメージから分かりやすく証明 スモビュ



グリーンの定理 積分定理の王 赤赤 新浪博客
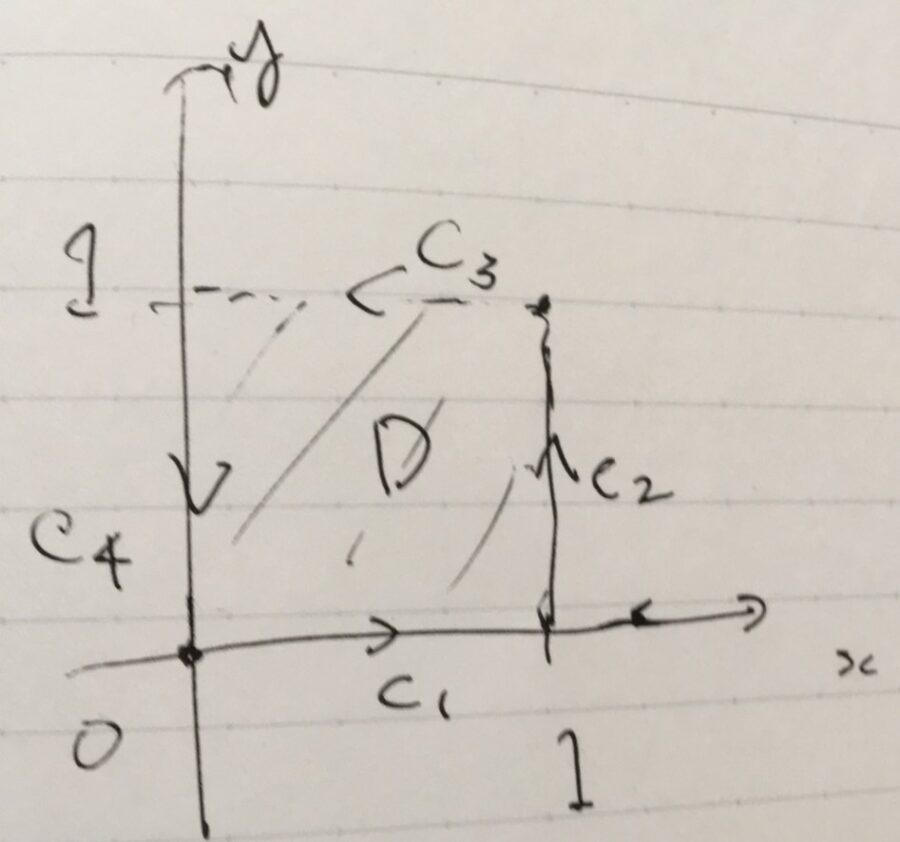



グリーンの定理の例による理解と証明 応用 趣味の大学数学
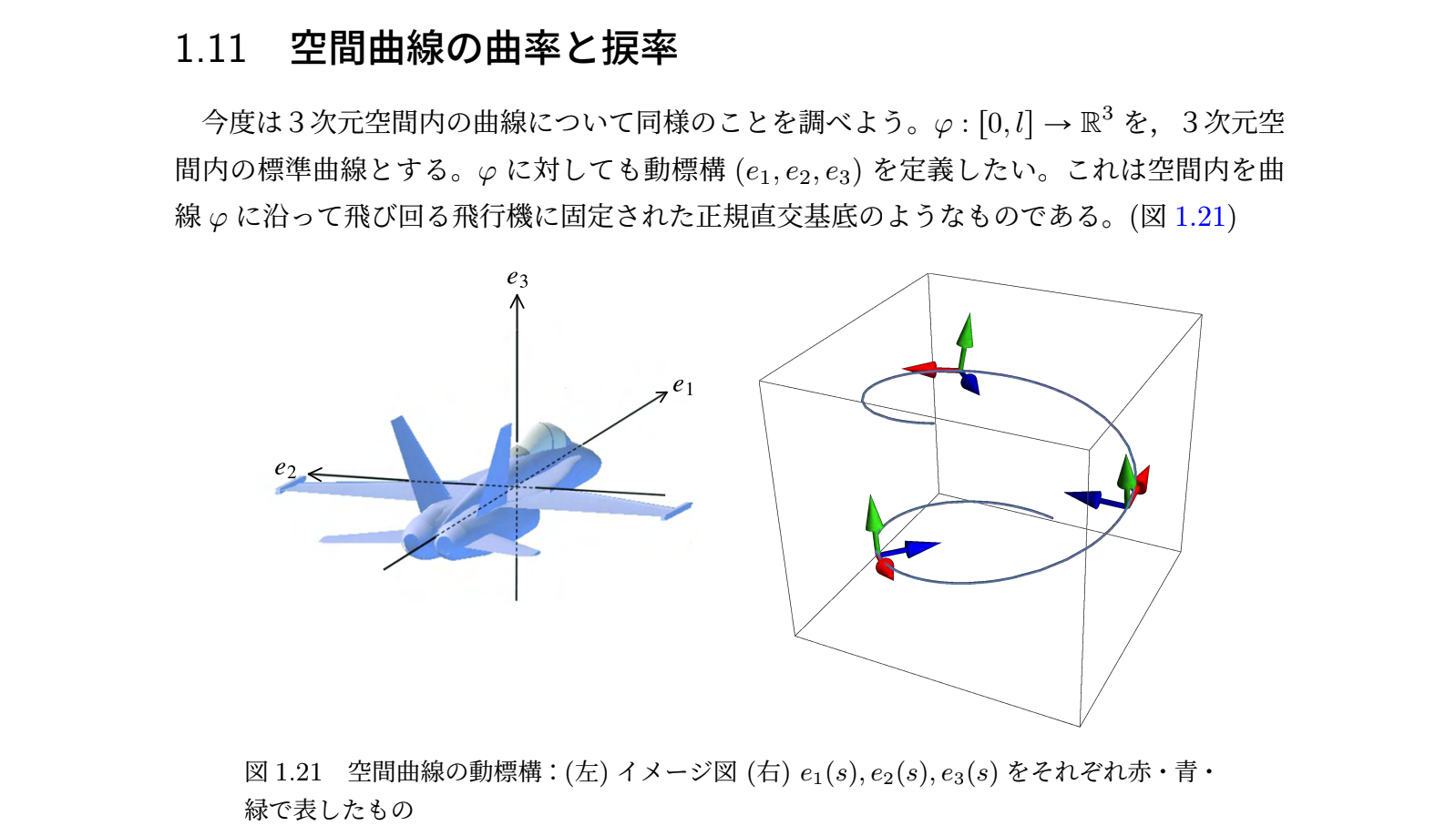



加藤晃史 先生 ベクトル解析 Utelecon



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配




グリーンの定理からコーシーの積分定理へ 身勝手な主張



ポアソン方程式 Poisson S Equation と波動方程式 Wave Equation




講師 幹 浩文 A314 Ta 西方良太 m1 A305 Ppt Download




単連結ではない領域のド ラームコホモロジー Tsujimotterのノートブック




高校数学a ガウス記号 X の方程式と不等式 受験の月




Paypayフリマ 数学セミナーリーディングス 定理からの数学入門 1984



テラスハウス ガウス グリーンの定理 理系 落ちこぼれkの東大受験日記



ベクトル解析 和から株式会社 大人のための数学教室




ガウスの法則 証明



媒介変数表示されたグラフの面積の求め方を例題付きで解説 検算に使える定理も教えます 東大医学部生の相談室




級数 Wikipedia




ベクトル解析の基礎 第2版 長谷川 正之 稲岡 毅 本 通販 Amazon




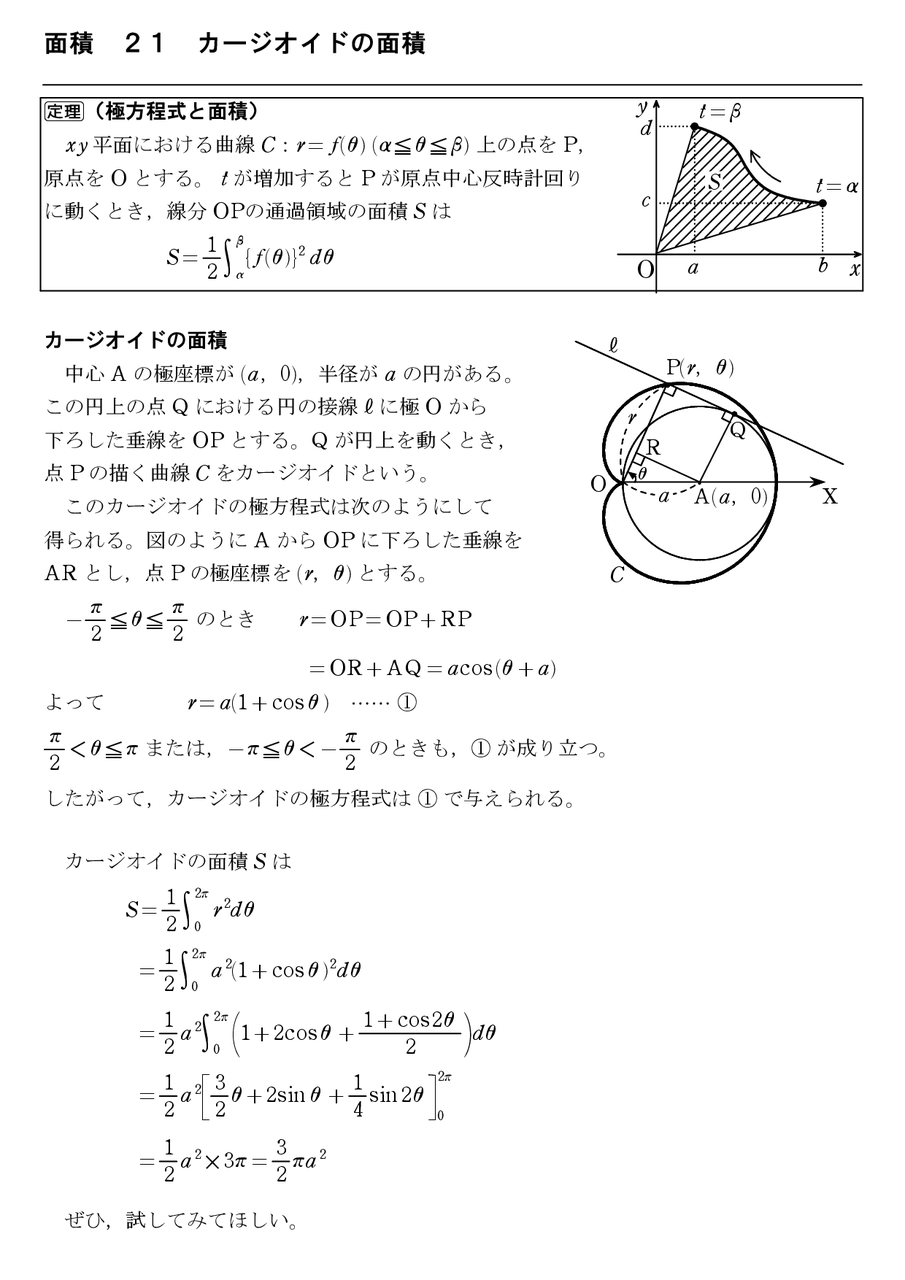
面積 22 ガウス積分 怜悧玲瓏 高校数学を天空から俯瞰する




Images Of グリーンの定理 Japaneseclass Jp




メルカリ 詳説演習 ベクトル解析 山内正敏著 参考書 300 中古や未使用のフリマ




有限要素法の手順とその原理に関する初歩的な質問 Okwave



グリーンの定理 積分定理の王 赤赤 新浪博客



グリーンの定理 積分定理の王




数値解析 積分定理の応用 大学生 専門学校生 社会人 数学のノート Clear



第13回 グリーン ガウス ストークスの定理




グリーンの定理




グリーンの定理からコーシーの積分定理へ 身勝手な主張



講師 幹 浩文 A314 Ta 西方良太 m1 A305 Ppt Download




ベクトル解析8 ガウスの発散定理 理系ノート



グリーンの定理 積分定理の王 赤赤 新浪博客




ガウスグリーンの定理の応用 Geogebra



数理科学 ノート




積分法 Wikipedia




ガウスグリーンの定理をわかりやすく解説 大学生 専門学校生 社会人 数学のノート Clear




飛鳥 そういえば昨日 中線定理の空間バージョン を見つけました



媒介変数表示されたグラフの面積の求め方を例題付きで解説 検算に使える定理も教えます 東大医学部生の相談室




媒介 変数 積分 積分の応用の問題



ガウスの発散定理をイメージで理解 Youtube




理系への数学 09年11月号 株式会社 現代数学社




書記が数学やるだけ 30 線積分とグリーンの定理で面積を求める 鈴華書記 Note




ガウスの法則 積分形 例題




第13回 グリーン ガウス ストークスの定理




受験生だけど数学の問題出してください




媒介 変数 積分 積分の応用の問題




ガウスの法則 証明




Images Of グリーンの定理 Japaneseclass Jp



授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する




B関数 G関数 勉強 Youtube スタディチューブ




ガウスグリーンの定理をわかりやすく解説 大学生 専門学校生 社会人 数学のノート Clear



0 件のコメント:
コメントを投稿